【题目】某天晚上,小春放学从学校步行回家,走了一段后,小春的同学小佳也从学校骑车回家,随后小佳追上了小春,并邀请小春坐他的自行车一起回家,但遭到了小春的拒绝.随后小佳便下车,推车与小春一起回家.很快小春到家了,小佳与小春道别后也骑上车继续回家.若学校、小春家、小佳家都在同一条笔直的公路上,则从小春出发时算起,小春与小佳的距离y关于时间t的函数图象最可能是下图中的( ).
A.  B.
B.  C.
C.  D.
D. 
参考答案:
【答案】B
【解析】
根据题意可对每个选项逐一分析判断图象得正误.
小春放学从学校步行回家,走了一段后,反映在函数图象上是一段上升的线段,小春的同学小佳也从学校骑车回家,说明小春与小佳的距离逐渐缩短,随后小佳追上了小春,并邀请小春坐他的自行车一起回家,但遭到了小春的拒绝.随后小佳便下车,推车与小春一起回家.很快小春到家了,说明小春与小佳的距离为0;小佳与小春道别后也骑上车继续回家,小春与小佳的距离逐渐拉大,由此可知选项B正确.
故选B .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ACB中,∠ACB=90゜,CD⊥AB于D.

(1)求证:∠ACD=∠B;
(2)若AF平分∠CAB分别交CD、BC于E、F,求证:∠CEF=∠CFE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(9分)已知如图(1):△ABC中,AB=AC,∠B、∠C的平分线相交于点O,过点O作EF∥BC分别交AB、AC于E、F.

(1)写出线段EF与BE、CF间的数量关系?(不证明)
(2)若AB≠AC,其他条件不变,如图(2),图中线段EF与BE、CF间是否存在(1)中数量关系?请说明理由.
(3)若△ABC中,AB≠AC,∠B的平分线与三角形外角∠ACD的平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F,如图(3),这时图中线段EF与BE,CF间存在什么数量关系?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(﹣1,0),与y轴的交点坐标为(0,3).
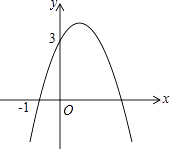
(1)求出b、c的值,并写出此二次函数的解析式;
(2)根据图象,直接写出函数值y为正数时,自变量x的取值范围;
(3)当2≤x≤4时,求y的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形纸片ABCD中,已知AB=6,BC=8,E是边AD上的点,以CE为折痕折叠纸片,使点D落在点F处,连接FC,当△AEF为直角三角形时,DE的长为________.
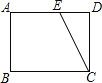
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,有一个等腰直角三角形AOB,∠OAB=90°,直角边AO在x轴上,且AO=1.将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1,且A1O=2AO,再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2,且A2O=2A1O…,依此规律,得到等腰直角三角形A2017OB2017.则点B2017的坐标是____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某建筑工程队利用一面墙(墙的长度不限),用40米长的篱笆围成一个长方形的仓库.

(1)求长方形的面积是150平方米,求出长方形两邻边的长;
(2)能否围成面积220平方米的长方形?请说明理由.
相关试题

