【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2.将△ABC绕点C顺时针旋转得到△A′B′C , 连结AB′.若A、B′、A′在同一条直线上,则AA′的长为( )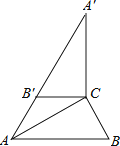
A.6
B.![]()
C.![]()
D.3
参考答案:
【答案】A
【解析】由在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,得
AB=4,∠BAC=30°.
由旋转的性质,得
A′B′=AB=4,∠A′=∠BAC=30°,∠A′B′C=∠B=60°,AC=A′C .
由等腰三角形的性质,得
∠CAB′=∠A′=30°.
由邻补角的定义,得
∠AB′C=180°-∠A′B′C=120°.
由三角形的内角和定理,得
∠ACB′=180°-∠AB′C-∠B′AC=30°.
∴∠B′AC=∠B′CA=30°,
AB′=B′C=BC=2.
A′A=A′B′+AB′=4+2=6,
故选:A.
【考点精析】掌握旋转的性质是解答本题的根本,需要知道①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程mx2-3x=x2-mx+2是关于x的一元二次方程,则m的取值范围为
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程ax2+bx+c=0(a≠0)有两个解为1和-1,则有a+b+c=;a-b+c=.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:a、b、c是△ABC的三边长,化简
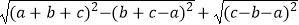 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】将方程5x﹣1=4x变形为5x﹣4x=1,这个过程利用的性质是( )
A. 等式性质1 B. 等式性质2
C. 移项 D. 以上说法都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年爷爷78岁,孙子24岁,(_______)年前爷爷的年龄是孙子的4倍.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=1,AC=2,现将△ABC绕点C顺时针旋转90°得到△A′B′C′ , 连接AB′,并有AB′=3,则∠A′的度数为( )
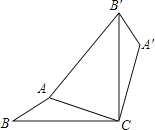
A.125°
B.130°
C.135°
D.140°
相关试题

