【题目】如图,在梯形ABCD中,AD∥BC,AC与BD交于O点,DO:BO=1:2,点E在CB的延长线上,如果S△AOD:S△ABE=1:3,那么BC:BE= . 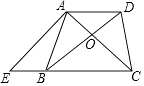
参考答案:
【答案】2:1
【解析】解:∵AD∥BC, ∴△AOD∽△COB,
∵DO:BO=1:2,
∴S△AOD:S△COB=1:4,S△AOD:S△AOB=1:2,
∵S△AOD:S△ABE=1:3,
∴S△ABC:S△ABE=6:3=2:1,
∴BC:BE=2:1.
【考点精析】本题主要考查了梯形的定义和相似三角形的判定与性质的相关知识点,需要掌握一组对边平行,另一组对边不平行的四边形是梯形.两腰相等的梯形是等腰梯形;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】课本的作业题中有这样一道题:把一张顶角为36°的等腰三角形纸片剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形,你能办到吗?请画示意图说明剪法. 我们有多少种剪法,图1是其中的一种方法:
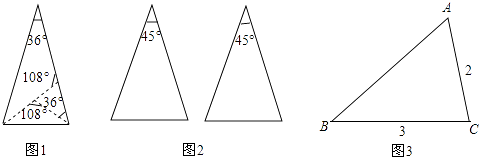
定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.
(1)请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数;(若两种方法分得的三角形成3对全等三角形,则视为同一种)
(2)△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,试画出示意图,并求出x所有可能的值;
(3)如图3,△ABC中,AC=2,BC=3,∠C=2∠B,请画出△ABC的三分线,并求出三分线的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】木匠黄师傅用长AB=3,宽BC=2的矩形木板做一个尽可能大的圆形桌面,他设计了四种方案:
方案一:直接锯一个半径最大的圆;
方案二:圆心O1、O2分别在CD、AB上,半径分别是O1C、O2A,锯两个外切的半圆拼成一个圆;
方案三:沿对角线AC将矩形锯成两个三角形,适当平移三角形并锯一个最大的圆;
方案四:锯一块小矩形BCEF拼到矩形AFED下面,利用拼成的木板锯一个尽可能大的圆.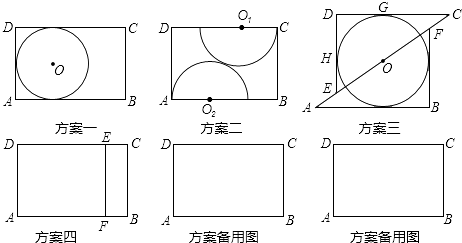
(1)写出方案一中圆的半径;
(2)通过计算说明方案二和方案三中,哪个圆的半径较大?
(3)在方案四中,设CE=x(0<x<1),圆的半径为y.
①求y关于x的函数解析式;
②当x取何值时圆的半径最大,最大半径为多少?并说明四种方案中哪一个圆形桌面的半径最大. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的腰长为6cm,底边长为4cm,以等腰三角形的顶角的顶点为圆心5cm为半径画圆,那么该圆与底边的位置关系是( )
A.相离
B.相切
C.相交
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=8,BC=6,D是AB的中点,点E在边AC上,将△ADE沿DE翻折,使得点A落在点A'处,当A'E⊥AC时,A'B= .
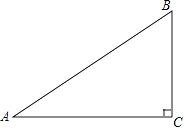
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是AB中点,联结CD.
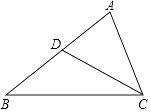
(1)若AB=10且∠ACD=∠B,求AC的长.
(2)过D点作BC的平行线交AC于点E,设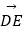 =
= 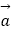 ,
, 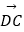 =
= 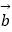 ,请用向量
,请用向量 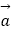 、
、 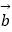 表示
表示 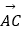 和
和 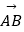 (直接写出结果)
(直接写出结果) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,CD⊥AB于点D,⊙D经过点B,与BC交于点E,与AB交与点F.已知tanA=
 ,cot∠ABC=
,cot∠ABC=  ,AD=8.
,AD=8. 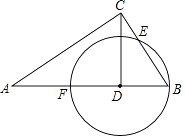
(1)⊙D的半径;
(2)CE的长.
相关试题

