【题目】如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )

A. ∠M=∠N B. AM=CN C. AB=CD D. AM∥CN
参考答案:
【答案】B
【解析】试题分析:根据普通三角形全等的判定定理,有AAS、SSS、ASA、SAS四种.逐条验证.
解:A、∠M=∠N,符合ASA,能判定△ABM≌△CDN,故A选项不符合题意;
B、根据条件AM=CN,MB=ND,∠MBA=∠NDC,不能判定△ABM≌△CDN,故B选项符合题意;
C、AB=CD,符合SAS,能判定△ABM≌△CDN,故C选项不符合题意;
D、AM∥CN,得出∠MAB=∠NCD,符合AAS,能判定△ABM≌△CDN,故D选项不符合题意.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以点P(-1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=
 ,将△ABC绕点P旋转180°,得到△MCB.
,将△ABC绕点P旋转180°,得到△MCB. 
(1)求B、C两点的坐标;
(2)请在图中画出线段MB、MC,并判断四边形ACMB的形状(不必证明),求出点M的坐标;
(3)动直线l从与BM重合的位置开始绕点B顺时针旋转,到与BC重合时停止,设直线l与CM交点为E,点Q为BE的中点,过点E作EG⊥BC于G,连接MQ、QG.请问在旋转过程中∠MQG的大小是否变化?若不变,求出∠MQG的度数;若变化,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某此数学考试中,(1)班有30%的同学成绩优秀,(2)班有36%的同学成绩优秀,则两班优秀同学的人数( )
A.(1)班多B.(2)班多C.一样多D.无法比较
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,射线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF。
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC∶∠OFC的值是否随之变化?若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由。

-
科目: 来源: 题型:
查看答案和解析>>【题目】逆定理的定义:一般地,如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,称这两个定理互为
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①A、E、F、C在一条直线上,AE=CF,过E、F分别作DE⊥AC,B F⊥AC,若AB=CD.
(1)图①中有 对全等三角形,并把它们写出来.
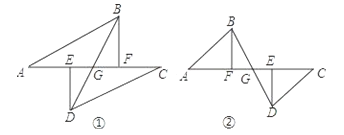
(2)求证:G是BD的中点.
(3)若将△ABF的边AF沿GA方向移动变为图②时,其余条件不变,第(2)题中的结论是否成立?如果成立,请予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x一元二次方程x2-x-m+2=0的两根x1,x2满足(x1-1)(x2-1)=-1,则m的值为( )
A. 3 B. -3 C. 2 D. -2
相关试题

