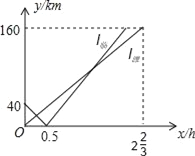
【题目】2015年5月中旬,中国和俄罗斯海军在地中海海域举行了代号为“海上联合﹣2015(1)”的联合军事演习,这是中国第一次地中海举行军事演习,也是这个海军距本土最远的一次军演,某天,“临沂舰”、“潍坊舰”两舰同时从A、B两个港口出发,均沿直线匀速驶向演习目标地海岛C,两舰艇都到达C岛后演习第一阶段结束,已知B刚位于A港、C港之间,且A、B、C在一条直线上,如图所示,l临、l潍分别表示“临沂舰”、“潍坊舰”离B港的距离行驶时间x(h)变化的图象.
(1)A港与C岛之间的距离为_____;
(2)分别求出“临沂舰”、“潍坊舰”的航速即相遇时行驶的时间;
(3)若“临沂舰”、“潍坊舰”之间的距离不超过2km时就属于最佳通讯距离,求出两舰艇在演习第一阶段处于最佳通讯距离时的x的取值范围.
参考答案:
【答案】(1)200km;(2)相遇时行驶的时间为2h;(3)![]() ≤x≤
≤x≤![]() .
.
【解析】
(1)从图象可以看出A港与C岛之间的距离为A、B间的距离+B、C间的距离就可以求出结论;
(2)根据A、B之间的距离和行驶时间可以求出其速度,就可以求出从B到C的时间,从而求出a,根据图象求出![]() 的解析式,然后由其解析式构成方程组求出其解就可以得出“临沂舰”、“潍坊舰”的航速即相遇时行驶的时间;
的解析式,然后由其解析式构成方程组求出其解就可以得出“临沂舰”、“潍坊舰”的航速即相遇时行驶的时间;
(2)分两种情况列出方程求出其解就可以得出答案.
解:(1)由图象,得
A港与C岛之间的距离为:200km;
故答案为:200km;
(2)“临沂舰”的航速:40÷0.5=80(km/h),
“潍坊舰”的航速:160÷2![]() =60(km/h),
=60(km/h),
所以“临沂舰”从A到C的时间a=0.5+160÷80=2.5,
设![]() 的解析式为y2=
的解析式为y2=![]() x,
x,![]() 的解析式为y1=k1x+b1,由图象得,
的解析式为y1=k1x+b1,由图象得,
160=2![]() ,
,![]() ,
,
解得:![]() =60,
=60,![]() ,
,
∴y2=60x,y1=80x﹣40,
当y1=y2时,
60x=80x﹣40,
x=2,
∴相遇时行驶的时间为2h;
(3)当y2﹣y1=2时,则60x﹣(80x﹣40)=2,
解得x=![]() ,
,
当y1﹣y2=2时,则(80x﹣40)﹣60x=2,
解得x=![]() ,
,
∴处于最佳通讯距离时的x的取值范围为![]() x
x![]() .
.
故答案为:(1)200km;(2)相遇时行驶的时间为2h;(3)![]() x
x![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知(x2+mx+1)(x2﹣2x+n)的展开式中不含x2和x3项.
(1)分别求m、n的值;
(2)化简求值:(m+2n+1)(m+2n﹣1)+(2m2n﹣4mn2+m3)÷(﹣m)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的直径CD垂直于弦AB,垂足为点E,∠ACD=22.5°,若CD=6cm,则AB的长为( )

A.4cm
B.3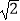 cm
cm
C.2 cm
cm
D.2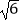 cm
cm -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
某商场用8万元购进一批新款衬衫,上架后很快销售一空,商场又紧急购进第二批这种衬衫,数量是第一次的2倍,但进价涨了4元/件,结果共用去17.6万元.
(1)该商场第一批购进衬衫多少件?
(2)商场销售这种衬衫时,每件定价都是58元,剩至150件时按八折出售,全部售完.售完这两批衬衫,商场共盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿EF折叠,点C落在A处,点D落在D′处.若AB=3,BC=9,则折痕EF的长为( )
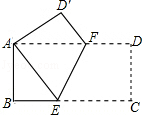
A.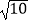
B.4
C.5
D.2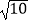
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+mx+m﹣2=0.
(1)求证:无论m取何值时,方程总有两个不相等的实数根;
(2)设方程两实数根分别为x1 , x2 , 且满足x12+x22=﹣3x1x2 , 求实数m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC和△DEC都是等腰直角三角形,C为它们的公共直角顶点,D、E分别在BC、AC边上.
(1)如图1,F是线段AD上的一点,连接CF,若AF=CF;
①求证:点F是AD的中点;
②判断BE与CF的数量关系和位置关系,并说明理由;
(2)如图2,把△DEC绕点C顺时针旋转α角(0<α<90°),点F是AD的中点,其他条件不变,判断BE与CF的关系是否不变?若不变,请说明理由;若要变,请求出相应的正确结论.

相关试题

