【题目】(1)化简![]() ;
;
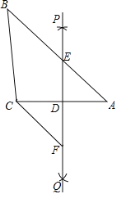
(2)如图,已知△ABC,按如下步骤作图:
①分别以A,C为圆心,大于![]() AC的长为半径画弧,两弧交于P, Q两点;
AC的长为半径画弧,两弧交于P, Q两点;
②作直线PQ,分别交AB,AC于点E,D;
③过C作CF∥AB交PQ于点F.
求证:△AED≌△CFD;
参考答案:
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)先把分子、分母分解因式,再约分即可;
(2)由作法知,PQ是线段AC的垂直平分线,从而可得AD=CD,由平行线的性质得∠A=∠DCF, ∠AED=∠CFD,然后根据“AAS”可证△AED≌△CFD.
(1)![]() =
=![]() ;
;
(2)由作法知,PQ是线段AC的垂直平分线,
∴AD=CD,
∵CF∥AB,
∴∠A=∠DCF, ∠AED=∠CFD,
在△AED和△CFD中,
∵∠A=∠DCF, ∠AED=∠CFD, AD=CD,
∴△AED≌△CFD(AAS),
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于抛物线
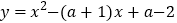 ,下列说法错误的是( )
,下列说法错误的是( )A. 开口向上 B. 当
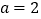 时,经过坐标原点O
时,经过坐标原点OC. 抛物线与x轴无公共点 D. 不论
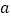 为何值,都过定点
为何值,都过定点 -
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》中记载了这样一个问题,大意为:有一个善于走路的人和一个不善于走路的人.善于走路的人走100步的同时,不善于走路的人只能走60步.现不善于走路的人先走100步,善于走路的人追他,则要走多少步才能追上(两人步长相等)?设善于走路的人走x步可追上,则可列方程为____________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠A=30°,AC=8,∠B=90°,点D在AB上,BD=
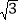 ,点P在△ABC的边上,则当AP=2PD时,PD的长为____________________.
,点P在△ABC的边上,则当AP=2PD时,PD的长为____________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校举行数学竞赛,对获一等奖的学生奖励数学家的著作《好玩的数学》,对获二等奖的学生奖励创意学生笔记本,若网购《好玩的数学》14元/本,创意学生笔记本12元/本,若《好玩的数学》数量比创意学生笔记本的数量的一半多5本,买两种奖品共用了1020元,购买两种奖品的数量各是多少本?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市中考必须在历史、地理、生物三门学科(分别用L、D、S表示)中随机抽考一门进行升学考试.
(1)用列举法写出连续两年抽考的情况;
(2)求连续两年抽到相同学科进行升学考试的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,等腰Rt△OAB的一条直角边OA 在x轴的正半轴上,点B在双曲线
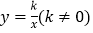 上,且∠BAO=90°,
上,且∠BAO=90°,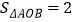 .
.(1)求k的值及点A的坐标;
(2)△OAB沿直线OB平移,当点A恰好在双曲线上时,求平移后点A的对应点A′的坐标.

相关试题

