【题目】已知抛物线y=-x2+bx+c的部分图象如图所示,A(1,0),B(0,3).
(1)求抛物线的解析式;
(2)结合函数图象,写出当y<3时x的取值范围.

参考答案:
【答案】(1)![]() ;(2)x<-2或x>0.
;(2)x<-2或x>0.
【解析】试题分析:
(1) 从题目中所给出的图象可知,点A和点B这两个已知点均在该二次函数图象上. 因此,可以将点A与点B的坐标代入二次函数解析式并组成方程组,求得待定系数b与c的值,进而获得该二次函数的解析式.
(2) 在题目所给出的图象上作直线y=3,该直线交二次函数图象于两点. 观察图象易知,满足y<3的二次函数图象应该在直线y=3的下方. 根据这部分图象横坐标的特点可知满足条件的横坐标分布范围. 由于该取值范围由直线y=3与二次函数交点的横坐标确定,故可以联立两个解析式解得交点坐标,进而求得x的取值范围.
试题解析:
(1) 由题目中的图象可知:该二次函数的图象过点A(1, 0),点B(0, 3),
将点A与点B的坐标代入二次函数的解析式,得
![]() ,即
,即![]() ,
,
解之,得
![]() ,
,
故该二次函数的解析式为![]() .
.
(2) 将题目中给出的二次函数图象适当延长,作直线y=3交二次函数图象于点B,C. (如图)
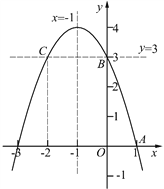
分析图象可知,满足y<3的二次函数图象应该是位于直线y=3下方的部分.
观察这部分图象上点的横坐标可知,对应y<3的x的取值应该小于点C的横坐标值或大于点B的横坐标值.
根据点B与点C均为该二次函数与直线y=3的交点可得下列方程组:
![]() ,
,
解这个方程组,得
![]() ,
,
![]() ,
,
∴x1=0,x2=-2.
即点B的坐标为(0, 3),点C的坐标为(-2, 3).
综上所述,当y<3时x的取值范围为x<-2或x>0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了节约用水,自来水公司对水价作出规定:当用水量不超过10吨时,每吨收费1.2元;当超过10吨时,超过部分每吨收费1.5元.某个月一户居民交费18元,则这户居民这个月用水多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x,y满足|x﹣3|+(y﹣6)2=0,则以x,y的值为两边长的等腰三角形的周长为( )
A. 12 B. 14 C. 15 D. 12或15
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)有一种可食用的野生菌,刚上市时,外商李经理以每千克30元的市场价格收购了这种野生菌1000千克存放入冷库中,据预测,该野生菌的市场价格将每天每千克上涨1元;但冷冻存放这批野生菌时每天需要支出各种费用合计310元,而且这种野生菌在冷库中最多保存140天,同时,平均每天有3千克的野生菌损坏导致不能出售.
(1)若存放
 天后,将这批野生菌一次性出售,设这批野生菌的销售总额为
天后,将这批野生菌一次性出售,设这批野生菌的销售总额为 元,试求出
元,试求出 与
与 之间的函数关系式;
之间的函数关系式;(2)李经理将这批野生菌存放多少天后一次性全部出售可以获得22500元的利润?
-
科目: 来源: 题型:
查看答案和解析>>【题目】求抛物线y=x2-2x的对称轴和顶点坐标,并画出图象.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
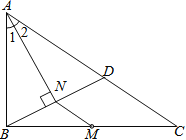
(1)求证:BN=DN;
(2)求△ABC的周长
相关试题

