【题目】如图,在![]() 中,AB=AC,以AC边为直径作⊙O交BC边于点D,过点D作
中,AB=AC,以AC边为直径作⊙O交BC边于点D,过点D作![]() 于点E,ED、AC的延长线交于点F.
于点E,ED、AC的延长线交于点F.
(1)求证:EF是⊙O的切线;
(2)若![]() 且
且![]() ,求⊙O的半径与线段AE的长.
,求⊙O的半径与线段AE的长.

参考答案:
【答案】(1)证明见解析;(2)⊙![]() 的半径长为
的半径长为![]() ,AE=
,AE=![]()
【解析】试题分析:(1)连结OD,如图,由AB=AC得到∠B=∠ACD,由OC=OD得到∠ODC=∠OCD,则∠B=∠ODC,于是可判断OD∥AB,然后利用DE⊥AB得到OD⊥EF,然后根据切线的判定定理得到结论;
(2)在Rt△ODF利用正弦的定义得到sin∠OFD=![]() ,则可设OD=3x,OF=5x,所以AB=AC=6x,AF=8x,在Rt△AEF中由于sin∠AFE=
,则可设OD=3x,OF=5x,所以AB=AC=6x,AF=8x,在Rt△AEF中由于sin∠AFE=![]() ,可得到AE=
,可得到AE=![]() x,接着表示出BE得到
x,接着表示出BE得到![]() x=
x=![]() ,解得x=
,解得x=![]() ,于是可得到AE和OD的长.
,于是可得到AE和OD的长.
试题解析:
(1)如图,连结![]() ,
,
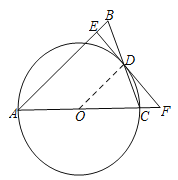
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() ∥
∥![]()
∵![]() ,
,
∴![]() .
.
∴![]() 是⊙
是⊙![]() 的切线
的切线
(2)在![]() 和
和![]() 中,
中,
∵![]() ,
,
∴![]() .
.
设![]() ,则
,则![]() .
.
∴![]() ,
, ![]()
∵![]() ,
,
∴![]()
∴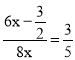 ,解得
,解得![]() =
=![]() ,
,
∴⊙![]() 的半径长为
的半径长为![]() ,
, ![]() =
=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】水位上升3米,记为+3米,水位下降2米,记为_________米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个大小不同的等腰直角三角形三角板如图①所示放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC,
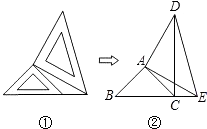
(1)请找出图②中的全等三角形,并给予说明(说明:结论中不得含有未标识的字母);
(2)试说明:DC⊥BE. -
科目: 来源: 题型:
查看答案和解析>>【题目】被历代数学家尊为“算经之首”的《九章算术》是中国古代算法的扛鼎之作.《九章算术》中记载:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”
译文:“今有
 只雀、
只雀、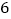 只燕,分别聚焦而且用衡器称之,聚在一起的雀重,燕轻.经一只雀、一只燕交换位置而放,重量相等.
只燕,分别聚焦而且用衡器称之,聚在一起的雀重,燕轻.经一只雀、一只燕交换位置而放,重量相等.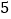 只雀、
只雀、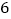 只燕重量为
只燕重量为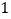 斤.问雀、燕每
斤.问雀、燕每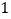 只各重多少斤?”
只各重多少斤?”请列方程组解答上面的问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.掷一枚硬币,正面一定朝上
B.某种彩票中奖概率为1%,是指买100张彩票一定有1张中奖
C.旅客上飞机前的安检应采用抽样调查
D.方差越大,数据的波动越大 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知2辆A型车和1辆B型车载满货物一次可运货10吨.用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆和B型车b辆,一次运完,且每辆车都满载货物.根据以上信息解答下列问题:
(1)1辆A型车和1辆B型车载满货物一次分别可运货物多少吨?
(2)请帮助物流公司设计租车方案
(3)若A型车每辆车租金每次100元,B型车每辆车租金每次120元.请选出最省钱的租车方案,并求出最少的租车费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若代数式3x2+5x的值为5,则代数式10x﹣9+6x2的值是( )
A. ﹣1B. 1C. 5D. 10
相关试题

