搜索
【题目】如图，AC和BD相交于O点，若OA=OD，用“SAS”证明△AOB≌△DOC还需（ ）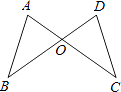 
A.AB=DC
B.OB=OC
C.∠C=∠D
D.∠AOB=∠DOC
参考答案：
【答案】B
【解析】解：A、AB=DC，不能根据SAS证两三角形全等，故本选项错误； B、∵在△AOB和△DOC中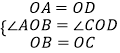
，
∴△AOB≌△DOC（SAS），故本选项正确；
C、两三角形相等的条件只有OA=OD和∠AOB=∠DOC，不能证两三角形全等，故本选项错误；
D、根据∠AOB=∠DOC和OA=OD，不能证两三角形全等，故本选项错误；
故选B．
添加AB=DC，不能根据SAS证两三角形全等；根据条件OA=OD和∠AOB=∠DOC，不能证两三角形全等；添加∠AOB=∠DOC，不能证两三角形全等；根据以上结论推出即可．
-
科目： 来源： 题型：
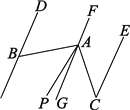
查看答案和解析>>【题目】如图，已知DB∥FG∥EC，A是FG上一点，∠ABD=60°，∠ACE=36°，AP平分∠BAC.
(1)请你求出∠BAC的度数；
(2)请你求出∠PAG的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，分别以点A和点B为圆心，大于
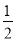AB长为半径画弧，两弧相交于点M、N，连接MN，交BC于点D，交AB于点E，连接AD．若△ABC的周长等于16，△ADC的周长为9，那么线段AE的长等于（ ）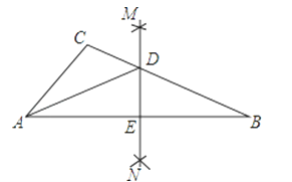
A. 3 B. 3.5 C. 5 D. 7
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，∠AOB的内部有一点P，在射线OA，OB边上各取一点P1 ， P2 ， 使得△PP1P2的周长最小，作出点P1 ， P2 ， 叙述作图过程（作法），保留作图痕迹．
-
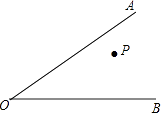
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中,AB//CD,∠ABC=∠ADC,DE垂直于对角线AC，垂足是E,连接BE .
（1）求证：四边形ABCD是平行四边形；
（2）若点E是AC的中点，判断BE与AC的位置关系，并说明理由；
（3）若△ABE是等边三角形，AD=
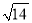,求对角线AC的长 .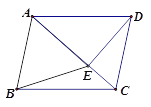
-
科目： 来源： 题型：
查看答案和解析>>【题目】若点A(3,3 )是正比例函数
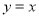上一点，点M(m ,0)与点N(0 ,n)分别在x轴与y轴上，且∠MAN=90°.（1）如图1，当N点与原点O重合，求M点的坐标；
（2）如图2，已知m,n都为正数，连接MN，若MN=
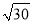，求△MON的面积.
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明不小心把一块三角形形状的玻璃打碎成了三块，如图①②③，他想要到玻璃店去配一块大小形状完全一样的玻璃，你认为应带（ ）
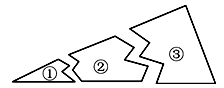
A. ① B. ② C. ③ D. ①和②
【答案】C
【解析】试题分析：根据全等三角形的判定方法带③去可以利用“角边角”得到全等的三角形．
故选C．
考点：全等三角形的应用．
【题型】单选题
【结束】
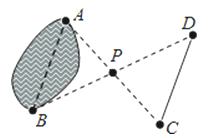
12【题目】如图，要测量池塘的宽度AB，在池塘外选取一点P，连接AP、BP并各自延长，使PC=PA，PD=PB，连接CD，测得CD长为25m，则池塘宽AB为________m，依据是________
相关试题
