【题目】如图,四边形ABCD是矩形,DG平分∠ADB交AB于点G,GF⊥BD于F.
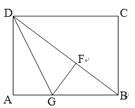
(1)求证:△ADG≌△FDG;(2)若BG=2AG,BD=2![]() ,求AD的长.
,求AD的长.
参考答案:
【答案】(1)证明见解析;(2)AD=![]() .
.
【解析】试题分析:(1)由矩形的性质和已知条件得出∠A=∠GFD,∠ADG=∠FDG,由AAS即可证明△AGD≌△FGD;
(2)由△AGD≌△FGD,得出对应边相等FG=AG,根据BG=2AG求出∠FBG=30°,根据直角三角形中30° 的角所对的边是斜边的一半即可求出.
试题解析:
(1)证明:∵四边形ABCD是矩形,GF⊥BD,
∴∠A=∠DFG=90°,
又∠ADG=∠FDG,DG=DG,
∴△ADG≌△FDG.
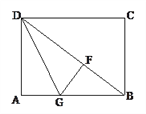
(2)解:由(1)得△ADG≌△FDG,
∴FG=AG,
∵BG=2AG,∴BG=2FG,
∴在Rt△BFG中,sin∠FBG=![]() ,
,
∴∠FBG=30°,
∴AD=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大家知道
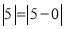 ,它在数轴上的意义是表示
,它在数轴上的意义是表示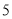 的点与原点(即表示
的点与原点(即表示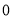 的点)之间的距离,又如式子
的点)之间的距离,又如式子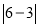 ,它在数轴上的意义是表示
,它在数轴上的意义是表示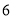 的点与表示
的点与表示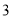 的点之间的距离.
的点之间的距离.(
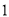 )在数轴上的意义是表示
)在数轴上的意义是表示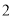 的点与表示
的点与表示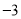 的点之间的距离是__________.
的点之间的距离是__________.(
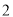 )反过来,式子
)反过来,式子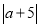 在数轴上的意义是__________.
在数轴上的意义是__________.(
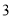 )试用数轴探究:当
)试用数轴探究:当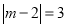 时,
时, 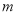 的值为__________.
的值为__________.(
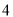 )进一步探究:
)进一步探究: 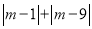 的最小值为__________.
的最小值为__________.(
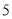 )最后发现:当
)最后发现:当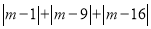 的值最小时,
的值最小时, 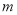 的值为__________.
的值为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,把两个全等的三角板ABC、EFG叠放在一起,使三角板EFG的直角边FG经过三角板ABC的直角顶点C,垂直AB于G,其中∠B=∠F=30°,斜边AB和EF均为4.现将三角板EFG由图1所示的位置绕G点沿逆时针方向旋转
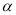 (0<
(0<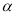 <90°),如图2,EG交AC于点K,GF交BC于点H.在旋转过程中,请你解决以下问题:
<90°),如图2,EG交AC于点K,GF交BC于点H.在旋转过程中,请你解决以下问题: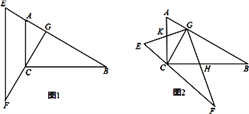
(1)求证:△CGH∽△AGK;
(2)连接HK,求证:KH∥EF;
(3)设AK=x,△CKH的面积为y,求y关于x的函数关系式,并求出y的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.所有的直角三角形都相似B.所有的等边三角形都相似
C.所有的矩形都相似D.所有的菱形都相似
-
科目: 来源: 题型:
查看答案和解析>>【题目】将多项式﹣2+4x2y+6x﹣x3y2按x的降幂排列: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 直线一定比射线长B. 过一点能作已知直线的一条垂线
C. 射线AB的端点是A和BD. 角的两边越长,角度越大
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个口袋中有3个大小相同的小球,球面上分别写有数字1、2、3.从袋中随机地摸出一个小球,记录下数字后放回,再随机地摸出一个小球.
(1)请用树形图或列表法中的一种,列举出两次摸出的球上数字的所有可能结果;
(2)求两次摸出的球上的数字和为偶数的概率.
相关试题

