【题目】如图,抛物线![]() (a、b、c为常数,a≠0)经过点A(﹣1,0),B(5,﹣6),C(6,0).
(a、b、c为常数,a≠0)经过点A(﹣1,0),B(5,﹣6),C(6,0).
(1)求抛物线的解析式;
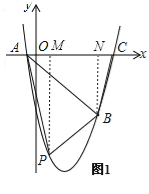
(2)如图,在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由;
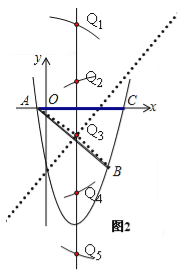
(3)若点Q为抛物线的对称轴上的一个动点,试指出△QAB为等腰三角形的点Q一共有几个?并请求出其中某一个点Q的坐标.

参考答案:
【答案】(1)![]() ;(2)P(2,﹣12);(3)这样的Q点一共有5个,如:Q3(
;(2)P(2,﹣12);(3)这样的Q点一共有5个,如:Q3(![]() ,
,![]() ).
).
【解析】(1)设y=a(x+1)(x﹣6)(a≠0),把B(5,﹣6)代入:a(5+1)(5﹣6)=﹣6,a=1,∴y=(x+1)(x﹣6),即![]() ;
;
(2)存在,如图1,分别过P、B向x轴作垂线PM和BN,垂足分别为M、N,设P(m,![]() ),四边形PACB的面积为S,则PM=
),四边形PACB的面积为S,则PM=![]() ,AM=m+1,MN=5﹣m,CN=6﹣5=1,BN=5,∴S=S△AMP+S梯形PMNB+S△BNC=
,AM=m+1,MN=5﹣m,CN=6﹣5=1,BN=5,∴S=S△AMP+S梯形PMNB+S△BNC=![]() =
=![]() =
=![]()
当m=2时,S有最大值为48,这时![]() =
=![]() =﹣12,∴P(2,﹣12);
=﹣12,∴P(2,﹣12);
(3)这样的Q点一共有5个,连接Q3A、Q3B,![]() =
=![]() ;
;
因为Q3在对称轴上,所以设Q3(![]() ,y),∵△Q3AB是等腰三角形,且Q3A=Q3B,由勾股定理得:
,y),∵△Q3AB是等腰三角形,且Q3A=Q3B,由勾股定理得:![]() ,解得:y=
,解得:y=![]() ,∴Q3(
,∴Q3(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】把抛物线y=﹣x2+4x﹣3先向左平移3个单位,再向下平移2个单位,则变换后的抛物线解析式是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正多边形的一个内角为135°,则该多边形的边数为( )
A.9
B.8
C.7
D.4 -
科目: 来源: 题型:
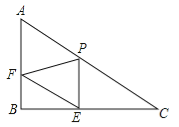
查看答案和解析>>【题目】已知Rt△ABC中,∠B=90°,AC=20,AB=10,P是边AC上一点(不包括端点A、C),过点P作PE⊥BC于点E,过点E作EF∥AC,交AB于点F.设PC=x,PE=y.
(1)求y与x的函数关系式;
(2)是否存在点P使△PEF是Rt△?若存在,求此时的x的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前,步行已成为人们最喜爱的健身方法之一,通过手机可以计算行走的步数与相应的能量消耗.对比手机数据发现小琼步行12000步与小博步行9000步消耗的能量相同.若每消耗1千卡能量小琼行走的步数比小博多10步,则小博每消耗1千卡能量需要行走________步.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,以点(﹣3,4)为圆心,4为半径的圆( )
A.与x轴相交,与y轴相切
B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交
D.与x轴相切,与y轴相离 -
科目: 来源: 题型:
查看答案和解析>>【题目】如下图。

(1)观察发现:如图1,已知Rt△ABC,∠ABC=90°,分别以AB,BC为边,向外作正方形ABDE和正方形BCFG,连接DG.若M是DG的中点,不难发现:BM= AC.
AC.
请完善下面证明思路:①先根据 ,证明BM=
,证明BM=  DG;②再证明
DG;②再证明  ,得到DG=AC;所以BM=
,得到DG=AC;所以BM=  AC;
AC;
(2)数学思考:若将上题的条件改为:“已知Rt△ABC,∠ABC=90°,分别以AB,AC为边向外作正方形ABDE和正方形ACHI,N是EI的中点”,则相应的结论“AN= BC”成立吗?小颖通过添加如图2所示的辅助线验证了结论的正确性.请写出小颖所添加的辅助线的作法,并由此证明该结论;
BC”成立吗?小颖通过添加如图2所示的辅助线验证了结论的正确性.请写出小颖所添加的辅助线的作法,并由此证明该结论;
(3)拓展延伸:如图3,已知等腰△ABC和等腰△ADE,AB=AC,AD=AE.连接BE,CD,若P是CD的中点,探索:当∠BAC与∠DAE满足什么条件时,AP= BE,并简要说明证明思路.
BE,并简要说明证明思路.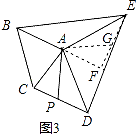
相关试题

