【题目】已知x1 , x2是方程x2﹣2x﹣1=0的两根,试求下列代数式的值.
(1)(x1+x2)(x1x2);
(2)(x1﹣x2)2 .
参考答案:
【答案】
(1)解:∵x1,x2是方程x2﹣2x﹣1=0的两根,
∴x1+x2=2,x1x2=﹣1.(x1+x2)(x1x2)=2+(﹣1)=1
(2)解:(x1﹣x2)2= ![]() ﹣4x1x2=22﹣4×(﹣1)=8
﹣4x1x2=22﹣4×(﹣1)=8
【解析】根据根与系数的关系可得出x1+x2=2、x1x2=﹣1.(1)将x1+x2=2、x1x2=﹣1代入即可得出结论;(2)利用完全平方公式将(x1﹣x2)2变形为 ![]() ﹣4x1x2 , 代入数据即可得出结论.
﹣4x1x2 , 代入数据即可得出结论.
【考点精析】本题主要考查了根与系数的关系的相关知识点,需要掌握一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生课外阅读的喜好,某校从八年级随机抽取部分学生进行问卷调查,调查要求每人只选取一种喜欢的书籍,如果没有喜欢的书籍,则作“其它”类统计.图(1)与图(2)是整理数据后绘制的两幅不完整的统计图.以下结论不正确的是( )


A. 由这两个统计图可知喜欢“科普常识”的学生有90人
B. 若该年级共有1200名学生,则由这两个统计图可估计喜爱“科普常识”的学生有360人
C. 由这两个统计图不能确定喜欢“小说”的人数
D. 在扇形统计图中,“漫画”所在扇形的圆心角为72°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.
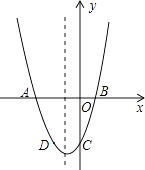
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)若抛物线上有一动点P,使三角形ABP的面积为6,求P点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】按要求解下列方程.
(1)(x﹣3)2=16
(2)x2﹣4x=5(配方法)
(3)x2﹣4x﹣5=0(公式法)
(4)x2﹣5x=0(因式分解法) -
科目: 来源: 题型:
查看答案和解析>>【题目】近几年某市加大中职教育投入力度,取得了良好的社会效果.某校随机调查了九年级m名学生的升学意向,并根据调查结果绘制出不完整的统计表如下:
升学意向
省级示范高中
市级示范高中
一般高中
职业高中
其他
合计
人数
15
15
9
3
m
百分比
25%
25%
n
5%
100%
请你根据统计表提供的信息解答下列问题:
(1)表中m的值为 ,n的值为 ;
(2)补全图7中的条形统计图;
(3)若该校九年级有学生500名,估计该校大约有多少名毕业生的升学意向是职业高中?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一个棱长为
 的正方体的每个面等分成
的正方体的每个面等分成 个小正方形,然后沿每个面正中心的一个正方形向里挖空(相当于挖去
个小正方形,然后沿每个面正中心的一个正方形向里挖空(相当于挖去 个小正方体),所得到的几何体的表面积是( )
个小正方体),所得到的几何体的表面积是( )
A. 78 B. 72 C. 54 D. 48
-
科目: 来源: 题型:
查看答案和解析>>【题目】当m为何值时,关于x的一元二次方程(2m+1)x2+4mx+2m﹣3=0.
(1)有两个不相等的实数根;
(2)有两个相等的实数根;
(3)没有实数根.
相关试题

