【题目】如图,直线l1的解析表达式为:y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1 , l2交于点C.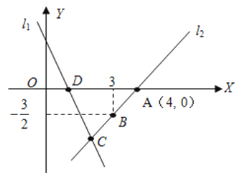
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积;
(4)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.
参考答案:
【答案】解:(1)由y=﹣3x+3,令y=0,得﹣3x+3=0,
∴x=1,
∴D(1,0);
(2)设直线l2的解析表达式为y=kx+b,
由图象知:x=4,y=0;x=3,y=-![]() ,代入表达式y=kx+b,
,代入表达式y=kx+b,
∴ 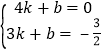 ,
,
∴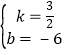 ,
,
∴直线l2的解析表达式为y=![]() x-6;
x-6;
(3)由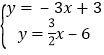 ,
,
解得![]() ,
,
∴C(2,﹣3),
∵AD=3,
∴S△ADC=![]() ×3×|﹣3|=
×3×|﹣3|=![]() ;
;
(4)△ADP与△ADC底边都是AD,面积相等所以高相等,△ADC高就是点C到直线AD的距离,即C纵坐标的绝对值=|﹣3|=3,
则P到AD距离=3,
∴P纵坐标的绝对值=3,点P不是点C,
∴点P纵坐标是3,
∵y=1.5x﹣6,y=3,
∴1.5x﹣6=3
x=6,
所以P(6,3).
【解析】(1)已知l1的解析式,令y=0求出x的值即可;
(2)设l2的解析式为y=kx+b,由图联立方程组求出k,b的值;
(3)联立方程组,求出交点C的坐标,继而可求出S△ADC;
(4)△ADP与△ADC底边都是AD,面积相等所以高相等,△ADC高就是点C到AD的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰但不等边的三角形的角平分线、高线、的总条数是( )
A.3 B.5 C.7 D.9
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,边长为4的正方形ABCD中,点E在AB边上(不与点A,B重合),点F在BC边上(不与点B,C重合).
第一次操作:将线段EF绕点F顺时针旋转,当点E落在正方形上时,记为点G;
第二次操作:将线段FG绕点G顺时针旋转,当点F落在正方形上时,记为点H;依次操作下去…
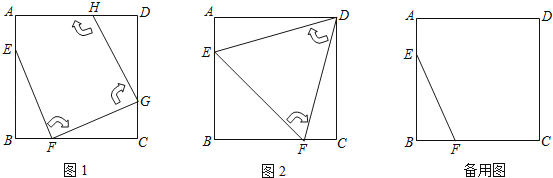
(1)图2中的△EFD是经过两次操作后得到的,其形状为 ,
(2)若经过三次操作可得到四边形EFGH.
①请判断四边形EFGH的形状为 ,此时AE与BF的数量关系是 ;
②以①中的结论为前提,设AE的长为x,四边形EFGH的面积为y,求y与x的函数关系式及面积y的取值范围。
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)已知 ,用含a,b的式子表示下列代数式。
,用含a,b的式子表示下列代数式。
①求: 的值 ②求:
的值 ②求:  的值
的值
(2)已知 ,求x的值.
,求x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算。
(1)若28n16n=222 , 求n的值.
(2)已知3m=6,9n=2,求32m﹣4n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列投影一定不会改变△ABC的形状和大小的是( )
A.中心投影
B.平行投影
C.正投影
D.当△ABC平行投影面时的平行投影 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.
(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.

相关试题

