【题目】如图,在△ADC中,AD=2,CD=4,∠ADC是一个不固定的角,以AC为边向△ADC的另一侧作等边三角形ABC,连接BD,则BD的长是否存在最大值?若存在,请求出其最大值;若不存在,请说明理由;

参考答案:
【答案】BD存在最大值,最大值是6.
【解析】
以AD为边做作等边三角形ADE,连接CE,根据等边三角形的性质和全等三角形的判定证明△ABD≌△ACE,再利用全等三角形的性质以及两点之间线段最短,即可证得结论.
证明:BD存在最大值;
如图,以AD为边做作等边三角形ADE,连接CE,
∵△ABC、△ADE都是等边三角形,
∴AB=AC,AD=AE=DE=2,∠BAC=∠EAD=60°,
∵∠BAD=∠BAC+∠DAC,∠EAC=∠EAD+∠DAC
∴∠BAD=∠EAC,且AB=AC,AD=AE
∴△ABD≌△ACE
∴BD=CE
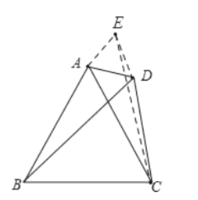
若点E,点D,点C不在一条直线上,则EC<ED+DC;
若点E,点D,点C在一条直线上,则EC=ED+DC.
∴EC≤ED+CD=2+4=6
∴BD≤6,
∴BD存在最大值,最大值是6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为响应“三节三爱”号召,我校把用电习惯分为“很注意节约用电(
 )”、“较注意节约用电(
)”、“较注意节约用电( )”“不注意节约用电(
)”“不注意节约用电( )”三类情况,设计了调查问卷在中学生中开展调查,并将调查结果分析整理后,制成如图所示的两个统计图.
)”三类情况,设计了调查问卷在中学生中开展调查,并将调查结果分析整理后,制成如图所示的两个统计图.
请根据以上信息解答下列问题:
(1)这次问卷调查共调查了多少名学生?其中“较注意节约用水”的学生有多少人?
(2)在扇形统计图中,“
 ”所对应的扇形的圆心角度数是多少?
”所对应的扇形的圆心角度数是多少?(3)如果设该校共有学生
 人,试估计“不注意节约用电”的学生人数.
人,试估计“不注意节约用电”的学生人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校环保志愿者协会对该市城区的空气质量进行调查,从全年365天中随机抽取了80天的空气质量指数(AQI)数据,绘制出三幅不完整的统计图表.请根据图表中提供的信息解答下列问题:
AQI指数
质量等级
天数(天)
0﹣50
优
m
51﹣100
良
44
101﹣150
轻度污染
n
151﹣200
中度污染
4
201﹣300
重度污染
2
300以上
严重污染
2
(1 )统计表中m= ,n= .扇形统计图中,空气质量等级为“良”的天数占 %;
(2)补全条形统计图,并通过计算估计该市城区全年空气质量等级为“优”和“良”的天数共多少天?
(3)据调查,严重污染的2天发生在春节期间,燃放烟花爆竹成为空气污染的一个重要原因,据此,请你提出一条合理化建议.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中∠ACB=90°,CD是AB边上的高,∠BAC的角平分线AF交CD于E,则△CEF必为( )

A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中∠B=45°,∠C=30°,点D为BC边上任意一点,连接AD,将线段AD绕A顺时针旋转90°,得到线段AE,连接DE.

(1)如图1,点E落在BA的延长线上时,∠EDC= (度)直接填空.
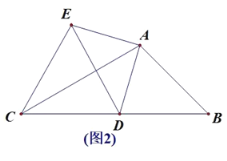
(2)如图2,点D在运动过程中,DE⊥AC时,AB=4 ,求DE的值.
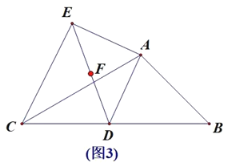
(3)如图3,点F为线段DE中点,AB=
 ,求出动点D从B运动到C,点F经过的路径长度.
,求出动点D从B运动到C,点F经过的路径长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:


请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小宇与小强两名男同学能分在同一组的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】适合下列条件的△ABC中,直角三角形的个数为( )
①a=3,b=4,c=5; ②a=6,∠A=45°;③a=2,b=2,c=2
 ; ④∠A=38°,∠B=52°.
; ④∠A=38°,∠B=52°.A. 1个 B. 2个 C. 3个 D. 4个
相关试题

