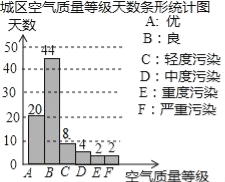
【题目】某学校环保志愿者协会对该市城区的空气质量进行调查,从全年365天中随机抽取了80天的空气质量指数(AQI)数据,绘制出三幅不完整的统计图表.请根据图表中提供的信息解答下列问题:
AQI指数 | 质量等级 | 天数(天) |
0﹣50 | 优 | m |
51﹣100 | 良 | 44 |
101﹣150 | 轻度污染 | n |
151﹣200 | 中度污染 | 4 |
201﹣300 | 重度污染 | 2 |
300以上 | 严重污染 | 2 |
(1 )统计表中m= ,n= .扇形统计图中,空气质量等级为“良”的天数占 %;
(2)补全条形统计图,并通过计算估计该市城区全年空气质量等级为“优”和“良”的天数共多少天?
(3)据调查,严重污染的2天发生在春节期间,燃放烟花爆竹成为空气污染的一个重要原因,据此,请你提出一条合理化建议.
参考答案:
【答案】(1)20,8,55;(2)答案见解析;292天;(3)答案见解析
【解析】
试题分析:(1)由A占25%,即可求得m的值,继而求得n的值,然后求得空气质量等级为“良”的天数占的百分比;(2)首先由(1)补全统计图,然后利用样本估计总体的知识求解即可求得答案;(3)提出合理建议,比如不燃放烟花爆竹或少燃放烟花爆竹等.
试题解析:(1)∵m=80×25%=20,n=80﹣20﹣44﹣4﹣2﹣2=8,
∴空气质量等级为“良”的天数占:![]() ×100%=55%.
×100%=55%.
(2)估计该市城区全年空气质量等级为“优”和“良”的天数共:365×(25%+55%)=292(天),
答:估计该市城区全年空气质量等级为“优”和“良”的天数共292天;
补全统计图:
(3)建议不要燃放烟花爆竹.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知 x1,x2是方程 x2-4x+3=0 的两个实数根,则x1 + x2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某篮球兴趣小组7名学生参加投篮比赛,每人投10个,投中的个数分别为:8,5,7,5,8,6,8,则这组数据的中位数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(3,y1)、B(4,y2)都在抛物线y=x2+1上,试比较y1与y2的大小:__________.
-
科目: 来源: 题型:
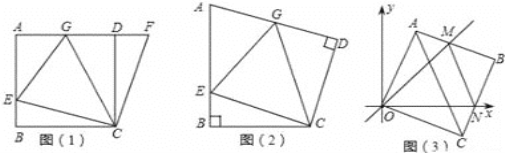
查看答案和解析>>【题目】如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.易证:CE=CF.
(1)在图1中,若G在AD上,且∠GCE=450.试猜想GE,BE,GD三线段之间的数量关系,并证明你的结论.
(2)运用(1)中解答所积累的经验和知识,完成下面两题:
①如图2,在四边形ABCD中∠B=∠D=900,BC=CD,点E,点G分别是AB边,AD边上的动点.若∠BCD=α,∠ECG=β,试探索当α和β满足什么关系时,图1中GE,BE,GD三线段之间的关系仍然成立,并说明理由.
②在平面直角坐标中,边长为1的正方形OABC的两顶点A,C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图3).设△MBN的周长为p,在旋转正方形OABC的过程中,p值是否有变化?若不变,请直接写出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向上平行行驶,那么两个拐弯的角度可能为 ( )
A. 先右转50°,后右转40° B. 先右转50°,后左转40°
C. 先右转50°,后左转130° D. 先右转50°,后左转50°
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x2+mx+8)(x2-3x+n)的展开式中不含x3和x2项,则mn的值是 .
相关试题

