【题目】如图1,2,3分别以△ABC的AB和AC为边向△ABC外作正三角形(等边三角形)、正四边形(正方形)、正五边形,BE和CD相交于点O.
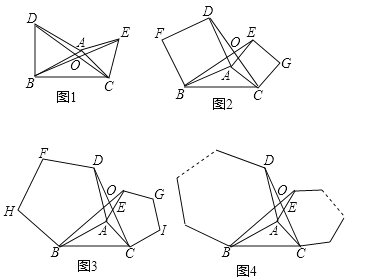
(1)在图1中,求证:△ABE≌△ADC.
(2)由(1)证得△ABE≌△ADC,由此可推得在图1中∠BOC=120°,请你探索在图2中,∠BOC的度数,并说明理由或写出证明过程.
(3)填空:在上述(1)(2)的基础上可得在图3中∠BOC= (填写度数).
(4)由此推广到一般情形(如图4),分别以△ABC的AB和AC为边向△ABC外作正n边形,BE和CD仍相交于点O,猜想得∠BOC的度数为 (用含n的式子表示).
参考答案:
【答案】(1)证明见解析;(2)∠BOC=90°;(3)72°;(4)![]() .
.
【解析】
试题分析:(1)根据等边三角形证明AB=AD,AC=AE,再利用等式性质得∠DAC=∠BAE,根据SAS得出△ABE≌△ADC;
(2)根据正方形性质证明△ABE≌△ADC,得∠BEA=∠DCA,再由正方形ACEG的内角∠EAC=90°和三角形外角和定理得∠BOC=90°;
(3)根据正五边形的性质证明:△ADC≌△ABM,再计算五边形每一个内角的度数为108°,由三角形外角定理求出∠BOC=72°;
(4)根据正n边形的性质证明:△ADC≌△ABM,再计算n边形每一个内角的度数为180°﹣![]() ,由三角形外角定理求出∠BOC=
,由三角形外角定理求出∠BOC=![]() .
.
试题解析:(1)如图1,∵△ABD和△ACE是等边三角形,∴AB=AD,AC=AE,∠DAB=∠EAC=60°,∴∠DAB+∠BAC=∠EAC+∠BAC,即∠DAC=∠BAE,∴△ABE≌△ADC;
(2)如图2,∠BOC=90°,理由是:
∵四边形ABFD和四边形ACGE都是正方形,∴AB=AD,AC=AE,∠DAB=∠EAC=90°,∴∠BAE=∠DAC,∴△ADC≌△ABE,∴∠BEA=∠DCA,∵∠EAC=90°,∴∠AMC+∠DCA=90°,∵∠BOC=∠OME+∠BEA=∠AMC+∠DCA,∴∠BOC=90°;
(3)如图3,同理得:△ADC≌△ABM,∴∠BME=∠DCA,∵∠BOC=∠BME+∠OEM=∠DCA+∠AEC,∵正五边形ACIGM,∴∠EAC=180°﹣![]() =108°,∴∠DCA+∠AEC=72°,∴∠BOC=72°;
=108°,∴∠DCA+∠AEC=72°,∴∠BOC=72°;
故答案为:72°;
(4)如图4,∠BOC的度数为![]() ,理由是:
,理由是:
同理得:△ADC≌△ABM,∴∠BME=∠DCA,∵∠BOC=∠BME+∠OEM=∠DCA+∠AEC,∵正n边形AC…M,∴∠EAC=180°﹣![]() ,∴∠DCA+∠AEC=180°﹣(180°﹣
,∴∠DCA+∠AEC=180°﹣(180°﹣![]() ),∴∠BOC=
),∴∠BOC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数y=(a+3)x+b-2的图像与x轴交于正半轴,与y轴交于负半轴,则( )
A. a>-3,b>2 B. a<-3,b<2 C. a>-3,b<2 D. a<-3,b>2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠CAB=50°,∠C=60°,求∠DAE和∠BOA的度数。

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算2a2+a2 , 结果正确的是( )
A.2a4
B.2a2
C.3a4
D.3a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】关于体育选考项目统计图
项目
频数
频率
A
80
b
B
c
0.3
C
20
0.1
D
40
0.2
合计
a
1

(1)求出表中a,b,c的值,并将条形统计图补充完整. 表中a= , b= , c= .
(2)如果有3万人参加体育选考,会有多少人选择篮球? -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小明遇到这样一个问题:如图1,△ABC中,AB=AC,点D在BC边上,∠DAB=∠ABD,BE⊥AD,垂足为E,求证:BC=2AE.
小明经探究发现,过点A作AF⊥BC,垂足为F,得到∠AFB=∠BEA,从而可证△ABF≌△BAE(如图2),使问题得到解决.
(1)根据阅读材料回答:△ABF与△BAE全等的条件是 AAS(填“SSS”、“SAS”、“ASA”、“AAS”或“HL”中的一个)
参考小明思考问题的方法,解答下列问题:
(2)如图3,△ABC中,AB=AC,∠BAC=90°,D为BC的中点,E为DC的中点,点F在AC的延长线上,且∠CDF=∠EAC,若CF=2,求AB的长;
(3)如图4,△ABC中,AB=AC,∠BAC=120°,点D、E分别在AB、AC边上,且AD=kDB(其中0<k<
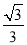 ),∠AED=∠BCD,求
),∠AED=∠BCD,求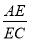 的值(用含k的式子表示).
的值(用含k的式子表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】-5+2-(-20)=( )
A.3
B.-3
C.17
D.2
相关试题

