【题目】已知等腰直角△ABC,∠C=90°,点D是斜边AB的中点,E是AC上的动点、∠EDF=90°,DF交BC 于点F.
(1)当 DE⊥AC,DF⊥BC 时,(如图1),我们很容易得出:S△DEF+S△CEF=![]() S△ABC.
S△ABC.
(2)如图2,DE与 AC不垂直,且点E在线段AC上时,(1)中的结论是否成立,如果不成立,请说明理由;如果成立,请证明.
(3)当点E运动到AC延长线上,其他条件不变,请把图3补充完整,直接写出 S△DEF,S△CEF,S△ABC的关系.

参考答案:
【答案】(1)证明见解析;(2)成立;证明见解析;(3)S△DEF﹣S△CEF=![]() S△ABC.
S△ABC.
【解析】
(1)根据三角形的中位线和正方形的性质即可得到结论;
(2)如图 2,过 D作 DM⊥AC于 M,DN⊥BC于 N,根据三角形的中位线大小在得到 DM=DN,推出四边形 CNDM是正方形,得到 S正方形 DMCN=![]() S△ABC, 根据余角的性质得到∠EDM=∠FDN,根据全等三角形的性质得到△EDM≌△FDN,于是得到结论;
S△ABC, 根据余角的性质得到∠EDM=∠FDN,根据全等三角形的性质得到△EDM≌△FDN,于是得到结论;
(2)如图 3,过 D作 DM⊥AC于 M,DN⊥BC于 N,根据三角形的中位线大小在得到DM=DN,推出四边形 CNDM是正方形,得到 S正方形 DMCN=![]() S△ABC,根据余角的性质得到∠EDM=∠FDN,根据全等三角形的性质得到△EDM≌△FDN,于是得到结论.
S△ABC,根据余角的性质得到∠EDM=∠FDN,根据全等三角形的性质得到△EDM≌△FDN,于是得到结论.
(1)∵DE⊥AC,DF⊥BC,
∴DE∥BC,DF∥AC,
∵点D是斜边AB的中点,AC=BC,
∴DE=DF=![]() AC,
AC,
∴EF=![]() AB,
AB,
∴S△DEF+S△CEF=S四边形 DECF=![]() S△ABC;
S△ABC;
(2)结论仍然成立,
证明:如图2,过D作DM⊥AC于M,DN⊥BC于N,

∴∠AMC=∠DNC=∠C=90°,
∴DM∥BC,DN∥AC,
∵点D是斜边AB的中点,
∴DM=![]() BC,DN=
BC,DN=![]() AC,
AC,
∴DM=DN,
∴四边形CNDM是正方形,
∴S正方形DMCN=![]() S△ABC,
S△ABC,
∵∠EDF=90°,
∴∠EDM=∠FDN,
在△EDM与△FDN中,
∴△EDM≌△FDN,(ASA),
∴S四边形CFDE=S正方形DMCN=S△DEF+S△CEF=![]() S△ABC;
S△ABC;
(3)如图3,

过D作DM⊥AC于M,DN⊥BC于N,
∴∠AMC=∠DNC=∠C=90°,
∴DM∥BC,DN∥AC,
∵点D是斜边AB的中点,
∴DM=![]() BC,DN=
BC,DN=![]() AC,
AC,
∴DM=DN,
∴四边形CNDM是正方形,
∴S正方形DMCN=![]() S△ABC,
S△ABC,
∵∠EDF=90°,
∴∠EDM=∠FDN,
在△EDM与△FDN中, ,
,
∴△EDM≌△FDN,(ASA),
∴S四边形CFDE=S正方形DMCN=S△DEF﹣S△CEF=![]() S△ABC.
S△ABC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:

(1)△AEF≌△CEB;
(2)AF=2CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)先化简
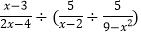 ,再任意选一个你喜欢的数作为x的值代入求值.
,再任意选一个你喜欢的数作为x的值代入求值.(2)先化简,再求值:
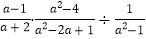 ,其中a2-a=0.
,其中a2-a=0.(3)已知y=
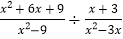 -x+3.试说明不论x为任何有意义的值,y的值均不变.
-x+3.试说明不论x为任何有意义的值,y的值均不变. -
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数分别填入相应的集合中:-(-230),
 ,0,-0.99,1.31,5,
,0,-0.99,1.31,5, ,3.14246792…,-
,3.14246792…,-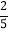 .
.(1)整数集合:{ …}
(2)非正数集合:{ …}
(3)正有理数集合:{ …}
(4)无理数集合:{ …}
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在x轴上方,∠BOA=90°且其两边分别与反比例函数y=﹣
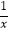 、y=
、y= 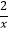 的图象交于B、A两点,则∠OAB的正切值为()
的图象交于B、A两点,则∠OAB的正切值为() 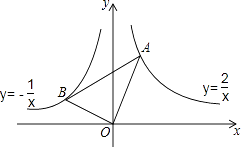
A.
B.
C.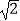
D.
-
科目: 来源: 题型:
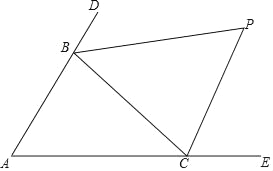
查看答案和解析>>【题目】如图,△ABC中,分别延长△ABC的边AB、AC到D、E,∠CBD与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业的时发现如下规律:
(1)若∠A=60°,则∠P= °;
(2)若∠A=40°,则∠P= °;
(3)若∠A=100°,则∠P= °;
(4)请你用数学表达式归纳∠A与∠P的关系 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工程队(有甲、乙两组)承包一项工程,规定若干天内完成.
①已知甲组单独完成这项工程所需时间比规定时间多30天,乙组单独完成这项工程所需时间比规定时间多12天,如果甲乙两组先合做20天,剩下的由甲组单独做,恰好按规定的时间完成,那么规定的时间是多少天?
②实际工作中,甲乙两组合做完成这项工程的
 后,工程队又承包了新工程,需要抽调一组过去,从按时完成任务考虑,你认为留下哪一组更好?说明理由.
后,工程队又承包了新工程,需要抽调一组过去,从按时完成任务考虑,你认为留下哪一组更好?说明理由.
相关试题

