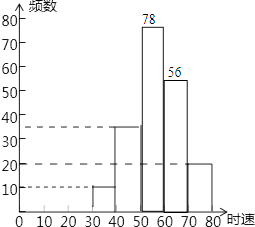
【题目】随着车辆的增加,交通违规的现象越来越严重,交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理(速度在30﹣40含起点值30,不含终点值40),得到其频数及频率如表:
数据段 | 频数 | 频率 |
30﹣40 | 10 | 0.05 |
40﹣50 | 36 | c |
50﹣60 | a | 0.39 |
60﹣70 | b | d |
70﹣80 | 20 | 0.10 |
总计 | 200 | 1 |
(1)表中a、b、c、d分别为:a=; b=; c=; d= .
(2)补全频数分布直方图;
(3)如果某天该路段约有1500辆通过,汽车时速不低于60千米即为违章,通过该统计数据估计当天违章车辆约有多少辆? 
参考答案:
【答案】
(1)78;0.18;0.28;56
(2)解:如图所示:
(3)解:违章车辆共有1500×(0.28+0.1)=570(辆).
答:当天违章车辆约有570辆.
【解析】(1)整理的车辆总数是:10÷0.05=200(辆),
则a=200×0.39=78,
c=36÷200=0.18;
d=1﹣0.18﹣0.39﹣0.10=0.28,
b=200×0.28=56.
故答案是:78;56;0.18;0.28.
【考点精析】本题主要考查了频数分布直方图的相关知识点,需要掌握特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图)才能正确解答此题.
-
科目: 来源: 题型:
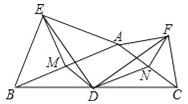
查看答案和解析>>【题目】如图,在钝角△ABC中,点D是BC的中点,分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和等腰直角三角形ACF,M、N分别为AB、AC的中点,连接DM、DN、DE、DF、EM、EF、FN.求证:
(1)△EMD≌△DNF;
(2)△EMD∽△EAF;
(3)DE⊥DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠CAB=130°,AB、AC的垂直平分线分别交BC于点E、F则∠EAF等于( )
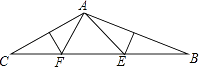
A.60°
B.70°
C.80°
D.90° -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:20022﹣2001×2003= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠MAN=135°,正方形ABCD绕点A旋转.
(1)当正方形ABCD旋转到∠MAN的外部(顶点A除外)时,AM,AN分别与正方形ABCD的边CB,CD的延长线交于点M,N,连接MN.
①如图1,若BM=DN,则线段MN与BM+DN之间的数量关系是 ;
②如图2,若BM≠DN,请判断①中的数量关系是否仍成立?若成立,请给予证明;若不成立,请说明理由;
(2)如图3,当正方形ABCD旋转到∠MAN的内部(顶点A除外)时,AM,AN分别与直线BD交于点M,N,探究:以线段BM,MN,DN的长度为三边长的三角形是何种三角形,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】设平面内一点到等边三角形中心的距离为d,等边三角形的内切圆半径为r,外接圆半径为R .对于一个点与等边三角形,给出如下定义:满足r≤d≤R的点叫做等边三角形的中心关联点.在平面直角坐标系xOy中,等边△ABC的三个顶点的坐标分别为A(0,2),B(﹣
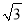 ,﹣1),C(
,﹣1),C(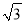 ,﹣1).
,﹣1).(1)已知点D(2,2),E(
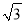 ,1),F(
,1),F(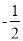 ,﹣1).在D,E,F中,是等边△ABC的中心关联点的是 ;
,﹣1).在D,E,F中,是等边△ABC的中心关联点的是 ;(2)如图1,过点A作直线交x轴正半轴于M,使∠AMO=30°.
①若线段AM上存在等边△ABC的中心关联点P(m,n),求m的取值范围;
②将直线AM向下平移得到直线y=kx+b,当b满足什么条件时,直线y=kx+b上总存在等边△ABC的中心关联点;(直接写出答案,不需过程)
(3)如图2,点Q为直线y=﹣1上一动点,⊙Q的半径为
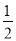 .当Q从点(﹣4,﹣1)出发,以每秒1个单位的速度向右移动,运动时间为t秒.是否存在某一时刻t,使得⊙Q上所有点都是等边△ABC的中心关联点?如果存在,请直接写出所有符合题意的t的值;如果不存在,请说明理由.
.当Q从点(﹣4,﹣1)出发,以每秒1个单位的速度向右移动,运动时间为t秒.是否存在某一时刻t,使得⊙Q上所有点都是等边△ABC的中心关联点?如果存在,请直接写出所有符合题意的t的值;如果不存在,请说明理由.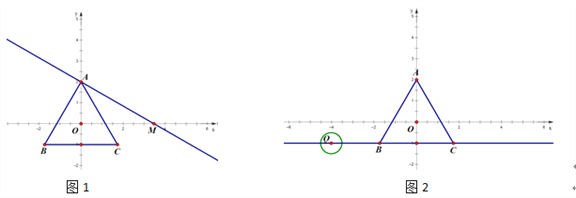
-
科目: 来源: 题型:
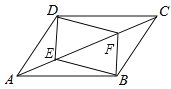
查看答案和解析>>【题目】如图,在ABCD中,点E,F在对角线AC上,且AE=CF.求证:
(1)DE=BF;
(2)四边形DEBF是平行四边形.
相关试题

