Question

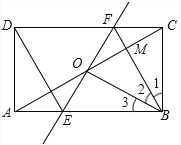
【题目】如图，矩形中，为中点，过点的直线分别与，交于点，，连接交于点，连接，．若，，则下列结论：

①，；

②；

③四边形是菱形；

④．

其中正确结论的个数是（ ）

A. 1 B. 2 C. 3 D. 4

Answer 1

【答案】C

【解析】

①证明△OBC是等边三角形，即可得OB=BC，由FO=FC，即可得FB垂直平分OC，①正确；②由FB垂直平分OC，根据轴对称的性质可得△FCB≌△FOB，根据全等三角形的性质可得∠BCF=∠BOF=90°，再证明△FOC≌△EOA，所以FO=EO，即可得OB垂直平分EF，所以△OBF≌△OBE，即△EOB≌△FCB，②错误；③证明四边形DEBF是平行四边形，再由OB垂直平分EF，根据线段垂直平分线的性质可得BE=BF，即可得平行四边形DEBF为菱形，③正确；④由OBF≌△EOB≌△FCB得∠1=∠2=∠3=30°，在Rt△OBE中，可得OE =OB，在Rt△OBM中，可得BM=OB，即可得BM ：OE =3：2，④正确.

①∵矩形ABCD中，O为AC中点，

∴OB=OC，

∵∠COB=60°，

∴△OBC是等边三角形，

∴OB=BC，

∵FO=FC，

∴FB垂直平分OC，

∴FB⊥OC，OM=CM；

①正确；

②∵FB垂直平分OC，

根据轴对称的性质可得△FCB≌△FOB，

∴∠BCF=∠BOF=90°，即OB⊥EF，

∵OA=OC，∠FOC=∠EOA，∠DCO=∠BAO，

∴△FOC≌△EOA，

∴FO=EO，

∴OB垂直平分EF，

∴△OBF≌△OBE，

∴△EOB≌△FCB，

②错误；

③∵△FOC≌△EOA，

∴FC=AE，

∵矩形ABCD，

∴CD=AB，CD∥AB，

∴DF∥EB，DF=EB，

∴四边形DEBF是平行四边形，

∵OB垂直平分EF，

∴BE=BF，

∴平行四边形DEBF为菱形；

③正确；

④由OBF≌△EOB≌△FCB得∠1=∠2=∠3=30°，

在Rt△OBE中，OE =OB，

在Rt△OBM中，BM=OB,

∴BM ：OE =OB：=OB=3：2.

④正确；

所以其中正确结论的个数为3个；

故选C.