【题目】如图,已知双曲线y= ![]() ,经过点D(6,1),点C是双曲线第三象限上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.
,经过点D(6,1),点C是双曲线第三象限上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC. 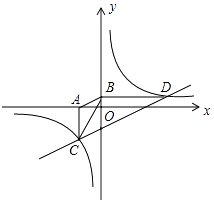
(1)求k的值;
(2)若△BCD的面积为12,求直线CD的解析式y1;
(3)根据图象直接写出y≥y1时,x的取值范围.
参考答案:
【答案】
(1)解:∵y= ![]() ,经过点D(6,1),
,经过点D(6,1),
∴ ![]() =1,
=1,
∴k=6;
(2)解:∵点D(6,1),
∴BD=6,
设△BCD边BD上的高为h,
∵△BCD的面积为12,
∴ ![]() BDh=12,即
BDh=12,即 ![]() ×6h=12,解得h=4,
×6h=12,解得h=4,
∴CA=3,
∴ ![]() =﹣3,解得x=﹣2,
=﹣3,解得x=﹣2,
∴点C(﹣2,﹣3),
设直线CD的解析式为y=kx+b,
则 ![]() ,
,
得  ,
,
所以,直线CD的解析式为y= ![]() x﹣2,
x﹣2,
(3)解:∵点D(6,1),点C(﹣2,﹣3),
∴当y≥y1时,x的取值范围为:x≤﹣2,0<x≤6.
【解析】(1)把点D的坐标代入双曲线解析式,进行计算即可得解;(2)先根据点D的坐标求出BD的长度,再根据三角形的面积公式求出点C到BD的距离,然后求出点C的纵坐标,再代入反比例函数解析式求出点C的坐标,然后利用待定系数法求一次函数解析式解答;(3)根据函数图象即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
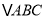 的内切圆
的内切圆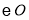 与
与 分别相切于点
分别相切于点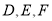 ,若
,若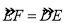 ,如图1.
,如图1.(1)判断
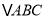 的形状,并证明你的结论;
的形状,并证明你的结论;(2)设
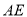 与
与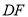 相交于点
相交于点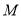 ,如图2,
,如图2,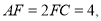 求
求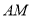 的长.
的长.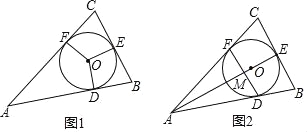
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列算式中,正确的是( )
A.2x+3y=5xy
B.3x2+2x3=5x5
C.4x﹣3x=1
D.x2﹣3x2=﹣2x2 -
科目: 来源: 题型:
查看答案和解析>>【题目】x=3是下列不等式( )的一个解.
A.x+1<0B.x+1<4C.x+1<3D.x+1<5
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级10个班师生举行毕业文艺汇演,每班2个节目,有歌唱与舞蹈两类节目,年级统计后发现歌唱类节目数比舞蹈类节目数的2倍少4个.
(1)九年级师生表演的歌唱与舞蹈类节目数各有多少个?
(2)该校七、八年级师生有小品节目参与,在歌唱、舞蹈、小品三类节目中,每个节目的演出平均用时分别是5分钟、6分钟、8分钟,预计所有演出节目交接用时共花15分钟.若从20:00开始,22:30之前演出结束,问参与的小品类节目最多能有多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣20﹣19=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知2x+3y-5=0,则9x27y的值为______.
相关试题

