【题目】某公司购进一种化工原料若干千克,价格为每千克30元,物价部门规定其销售单价每千克不高于60元且不低于30元,经市场调查发现,日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时,y=80,当x=50时,y=100.
(1)求y与x的函数解析式;
(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数解析式;
(3)求当销售单价为多少元时,该公司日获利最大?最大利润是多少元?
参考答案:
【答案】(1)y=﹣2x+200(30≤x≤60);(2)w=﹣2x2+260x﹣6000;(3)当销售单价为60元时,该公司日获利最大,最大利润是2400元.
【解析】
试题分析:(1)根据日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时,y=80,当x=50时,y=100,可以求得y与x的函数解析式;
(2)根据公司购进一种化工原料若干千克,价格为每千克30元,物价部门规定其销售单价每千克不高于60元且不低于30元,和第一问中求得的y与x的函数解析式,可以求得该公司销售该原料日获利w(元)与销售单价x(元)之间的函数解析式;
(3)将第(2)问中的函数解析式化为顶点式,然后根据二次项系数和对称轴和x的取值范围可以确定当销售单价为多少元时,该公司日获利最大,最大利润是多少元.
解;(1)由题意可得,设y与x的函数解析式是:y=kx+b,
∵当x=60时,y=80,当x=50时,y=100,
∴![]() ,
,
解得k=﹣2,b=200.
即y与x的函数解析式是:y=﹣2x+200(30≤x≤60);
(2)由题意可得,
w=(x﹣30)(﹣2x+200)=﹣2x2+260x﹣6000,
即该公司销售该原料日获利w(元)与销售单价x(元)之间的函数解析式是:w=﹣2x2+260x﹣6000;
(3)∵w=﹣2x2+260x﹣6000
∴w=﹣2(x﹣65)2+2450
∴当x<65时,y随x的增大而增大,
∵30≤x≤60,
∴当x=60时,w取得最大值,此时w=﹣2(60﹣65)2+2450=2400(元),
即当销售单价为60元时,该公司日获利最大,最大利润是2400元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某天的温度上升了-2℃的意义是 ( )
A.上升了2℃ B.没有变化
C.下降了-2℃ D.下降了2℃
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a、b、c为三角形的三边,化简|a﹣b+c|+|a﹣b﹣c|+|c﹣b﹣a|=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某赛季甲、乙两名篮球运动员12场比赛得分情况用图表示如下:对这两名运动员的成绩进行比较,下列四个结论中,不正确的是( )
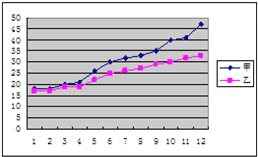
A.甲运动员得分的极差大于乙运动员得分的极差
B.甲运动员得分的中位数小于乙运动员得分的中位数
C.甲运动员的得分平均数大于乙运动员的得分平均数
D.乙运动员的成绩比甲运动员的成绩稳定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图两个同心圆,大圆的半径为5,小圆的半径为1,若大圆的弦AB与小圆有公共点,则弦AB的取值范围是( )
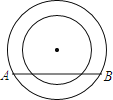
A.8≤AB≤10 B.8<AB≤10 C.4≤AB≤5 D.4<AB≤5
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知4个矿泉水空瓶可以换矿泉水一瓶,现有16个矿泉水空瓶,若不交钱,最多可以喝矿泉水( )
A. 3瓶 B. 4瓶 C. 5瓶 D. 6瓶
-
科目: 来源: 题型:
查看答案和解析>>【题目】随州市尚市“桃花节”观赏人数逐年增加,据有关部门统计,2014年约为20万人次,2016年约为28.8万人次,设观赏人数年均增长率为x,则下列方程中正确的是( )
A.20(1+2x)=28.8
B.28.8(1+x)2=20
C.20(1+x)2=28.8
D.20+20(1+x)+20(1+x)2=28.8
相关试题

