【题目】阅读下面材料:
小敏遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=5,求BC+DE的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使
问题得到解决(如图2).
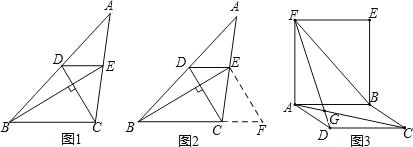
(1)请回答:BC+DE的值为 .
(2)参考小明思考问题的方法,解决问题:
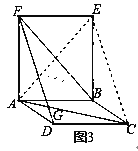
如图3,已知ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠AGF的度数.
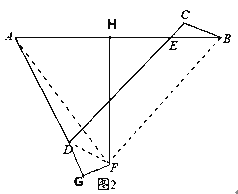
如图4,已知:AB、CD交于E点,连接AD、BC,AD=3![]() ,BC=1.且∠B与∠D互为余角,∠A与∠C互为补角,则∠AED= 度,若CD=
,BC=1.且∠B与∠D互为余角,∠A与∠C互为补角,则∠AED= 度,若CD=![]() ,求AB的长.
,求AB的长.

参考答案:
【答案】(1)![]() ;(2)∠AGF=60°,∠AED=45°,AB=7
;(2)∠AGF=60°,∠AED=45°,AB=7
【解析】试题分析:(1)由DE∥BC,EF∥DC,可证得四边形DCFE是平行四边形,求出DE=CF,DC=EF,由DC⊥BE,四边形DCFE是平行四边形,可得Rt△BEF,求出BF的长,证明BC+DE=BF;
(2)首先连接AE,CE,由四边形ABCD是平行四边形,四边形ABEF是矩形,易证得四边形DCEF是平行四边形,继而证得△ACE是等边三角形,则可求得答案.
以CD、CB为邻边作平行四边形BCDF,则有∠ABF=∠AED=45°,BF=DC=4![]() ,通过解直角三角形求解即可.
,通过解直角三角形求解即可.
试题解析:(1)∵DE∥BC,EF∥DC,
∴四边形DCFE是平行四边形,
∴EF=CD=3,CF=DE,
∵CD⊥BE,
∴EF⊥BE,
∴BC+DE=BC+CF=BF=![]()
(2)解决问题:连接AE,CE,如图.
∵四边形ABCD是平行四边形,
∴AB∥DC.
∵四边形ABEF是矩形,
∴AB∥FE,BF=AE.
∴DC∥FE.
∴四边形DCEF是平行四边形.
∴CE∥DF.
∵AC=BF=DF,
∴AC=AE=CE.
∴△ACE是等边三角形.
∴∠ACE=60°.
∵CE∥DF,
∴∠AGF=∠ACE=60°.
∵∠B与∠D互为余角,∠A与∠C互为补角,
∴∠D+∠B=90°,∠A+∠C=180°.
∵∠A+∠D+∠AED=180°,
∠B+∠C+∠BEC=180°,
∴∠A+∠D+∠AED+∠B+∠C+∠BEC=360°.
∴∠AED+∠BEC+90°+180°=360°.
∴∠AED+∠BEC=90°.
∵∠AED=∠BEC,
∴∠AED=∠BEC=45°.
以CD、CB为邻边作平行四边形BCDF,连接AF,如图2所示,
∵四边形BCDF是平行四边形,
∴BF=DC=4![]() ,DF=BC=1,∠DFB=∠C=180°﹣∠DAB,DC∥BF.
,DF=BC=1,∠DFB=∠C=180°﹣∠DAB,DC∥BF.
∴∠ABF=∠AED=45°.
在四边形ABFD中,
∵∠DAB+∠ABF+∠BFD+∠ADF=360°,∠DFB=180°﹣∠DAB,∠ABF=45°,
∴∠ADF=135°.
DF=1 , DG=FG=![]()
在△AGF中,
∵AG=3.5![]() ,DG=
,DG=![]() ,∠G=90°,
,∠G=90°,
∴AF=5
BF=4![]() ,FH=BH=4,AF=5,AH=3
,FH=BH=4,AF=5,AH=3
∴AB的长为7.
-
科目: 来源: 题型:
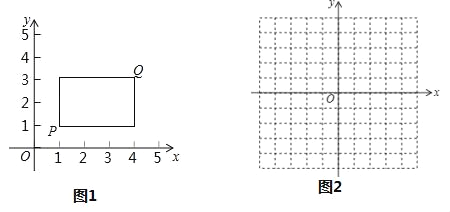
查看答案和解析>>【题目】在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2,若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,如图为点P,Q的“相关矩形”示意图.
(1)已知点A的坐标为(1,0),
①若点B的坐标为(3,1),求点A,B的“相关矩形”的面积;
②点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(2)正方形RSKT顶点R的坐标为(-1,1),K的坐标为(2,-2),点M的坐标为(m,3),若在正方形RSKT边上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某蓄水池的横断面示意图如图所示,分深水区和浅水区,如果这个注满水的蓄水池以固定的流量把水全部放出,下面的图象能大致表示水的深度h和放水时间t之间的关系的是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=x+2与y=-2x+6的图象相交于点A,函数y=-2x+6的图象分别交x轴、y轴于点B、C,函数y=x+2的图象分别与x轴、y轴交于点E、D.
(1)求点A的坐标;
(2)求△ABE的面积.
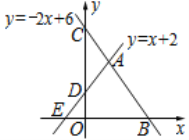
-
科目: 来源: 题型:
查看答案和解析>>【题目】在墙上固定一根木条,至少需要钉两颗钉子.能解释这一实际应用的数学知识是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一商店在某时间以每件480元的价格卖出两件衣服,其中一件盈利20%,另一件亏损20%,卖这两件衣服是盈利还是亏损,或是不盈不亏?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,∠A的平分线交DC于E,若∠DEA=30°,则∠B=( ).
A. 100° B. 120° C. 135° D. 150°
相关试题

