【题目】如图,海中一渔船在A处与小岛C相距70海里,若该渔船由西向东航行30海里到达B处,此时测得小岛C位于B的北偏东30°方向上,则该渔船此时与小岛C之间的距离是_____海里.
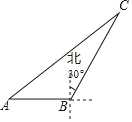
参考答案:
【答案】50
【解析】分析:过点C作CD⊥AB于点D,由题意得∠BCD=30°,设BC=x,解直角三角形即可得到BD、CD,进而得出AD,根据“AD2+CD2=AC2”列方程求解可得.
详解:过点C作CD⊥AB于点D,
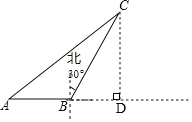
由题意得∠BCD=30°,
设BC=x,
在Rt△BCD中,
BD=BCsin30°=![]() x,CD=BCcos30°=
x,CD=BCcos30°=![]() x;
x;
∴AD=30+![]() x,
x,
∵AD2+CD2=AC2,
∴(30+![]() x)2+(
x)2+(![]() x)2=702,
x)2=702,
解得:x=50(负值舍去),
即渔船此时与C岛之间的距离为50海里.
故答案为:50.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将平行四边形ABCD折叠,使顶点D恰好落在AB边上的点M处,折痕为AN,有以下四个结论①MN∥BC;②MN=AM;③四边形MNCB是矩形;④四边形MADN是菱形,以上结论中,你认为正确的有_____________(填序号).
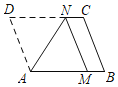
-
科目: 来源: 题型:
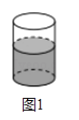
查看答案和解析>>【题目】有一个盛水的圆柱体玻璃容器,它的底面半径为
 (容器厚度忽略不计),容器内水的高度为
(容器厚度忽略不计),容器内水的高度为 .
.(1)如图1, 容器内水的体积为_
 (结果保留
(结果保留 ).
).
(2)如图2,把一根半径为
 ,高为
,高为 的实心玻璃棒插入水中(玻璃棒完全淹没于水中),求水面上升的高度是多少?
的实心玻璃棒插入水中(玻璃棒完全淹没于水中),求水面上升的高度是多少?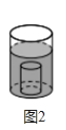
(3)如图3,若把一根半径为
 ,足够长的实心玻璃棒插入水中,求水面上升的高度是多少?
,足够长的实心玻璃棒插入水中,求水面上升的高度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,每个小正方形的边长为1cm
(1)求四边形ABCD的面积;
(2)四边形ABCD中有直角吗?若有,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l:y=
 x﹣
x﹣ 与x轴交于点B1,以OB1为一边在OB1上方作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为一边在A1B2上方作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为一边在A2B3上方作等边三角形A3A2B3,…,则△A2017B2018A2018的周长是_____.
与x轴交于点B1,以OB1为一边在OB1上方作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为一边在A1B2上方作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为一边在A2B3上方作等边三角形A3A2B3,…,则△A2017B2018A2018的周长是_____.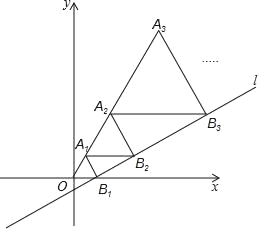
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF,求证:四边形ADCF是菱形.

-
科目: 来源: 题型:
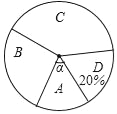
查看答案和解析>>【题目】我市某中学举行演讲比赛,赛后整理参赛学生的成绩,将比赛成绩分为A,B,C,D四个等级,把结果列成下表(其中,m是常数)并绘制如图所示的扇形统计图(部分).
等级
A
B
C
D
人数
6
10
m
8
(1)求m的值和A等级所占圆心角α的大小;
(2)若从本次比赛中获得A等级的学生中,选出2名取参加市中心学生演讲比赛,已知A等级中男生有2名,求出所选2名学生中恰好是一名男生和一名女生的概率.
相关试题

