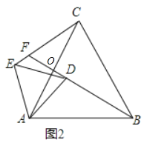
【题目】如图,△ABC是边长为6的等边三角形,点D、E分别是边AB、AC的中点,将△ADE绕点A旋转,BD与CE所在的直线交于点F.
(1)如图(2)所示,将△ADE绕点A逆时针旋转,且旋转角不大于60°,∠CFB的度数是多少?说明你的理由?
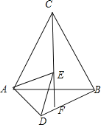
(2)当△ADE绕点A旋转时,若△BCF为直角三角形,求出线段BF的长.

参考答案:
【答案】(1)∠CFB=60°,理由见解析;(2)4![]() 或2
或2![]() .
.
【解析】
(1)根据等边三角形的性质得到AC=AB,∠EAD=∠CAB=60°,由点D、E分别是边AB、AC的中点,得到AE=AD,根据旋转的性质得到∠EAC=∠BAD,根据全等三角形的性质得到∠ACE=∠ABD,由对顶角相等得∠COF=∠AOB,根据三角形的内角和即可得到结论;
(2)根据含30°角的直角三角形的性质,利用勾股定理解直角三角形,分两种情况求解即可得到结论.
解:(1)∠CFB=60°,
理由:∵△ABC是等边三角形,
∴AC=AB,∠CAB=60°,
∵点D、E分别是边AB、AC的中点,
∴![]()
∴AE=AD,
∵将△ADE绕点A旋转,BD与CE所在的直线交于点F,
∴∠EAC=∠BAD,
在△ACE与△ABD中,
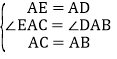 ,
,
∴△ACE≌△ABD,
∴∠ACE=∠ABD,设AC交BF于O,
∵∠COF=∠AOB,
∴∠CFB=∠CAB=60°;
(2)∠CFB=60°,∠BCF=90°时,∠CBF=30°,
∴CF =![]() BF,
BF,![]()
∴![]() ,
,
解得:BF=4![]() ;
;
∠CFB=60°,∠CBF=90°时,∠BCF=30°,
∴CF =2BF,![]()
∴![]()
解得:BF = 2![]() .
.
故答案为:(1)∠CFB=60°,理由见解析;(2)4![]() 或2
或2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入它所属的集合内:
3,200%,
 ,|2|,0,5.32,2.333….
,|2|,0,5.32,2.333….(1)整数集合:

 ;
;(2)分数集合:

 ;
;(3)非负数集合:

 ;
; -
科目: 来源: 题型:
查看答案和解析>>【题目】教师节当天,出租车司机小王在东西向的街道上免费接送教师,规定向东为正,向西为负,当天出租车的行程如下(单位:千米)
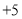 ,
,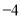 ,
,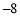 ,
,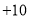 ,
,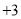 ,
,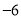 ,
,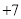 ,
,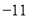 .
.(1)将最后一名老师送到目的地时,小王距出发地多少千米?
(2)若汽车耗油量为0.5升/千米,则当天耗油多少升?若汽油价格为6.70元/升,则小王共花费了多少元钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列两个等式:
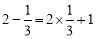 ,
, ,给出定义如下:我们称使等式
,给出定义如下:我们称使等式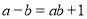 成立的一对有理数“
成立的一对有理数“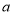 ,
, ”为“共生有理数对”,记为(
”为“共生有理数对”,记为(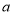 ,
, ).
).(1)通过计算判断数对“2,1,“4,
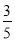 ”是不是“共生有理数对”;
”是不是“共生有理数对”;(2)若(6,a)是“共生有理数对”,求a的值;
(3)若(m,n)是“共生有理数对”,则“n,m”___“共生有理数对”(填“是”或“不是”),并说明理由;
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平行四边形ABCD中,CE平分∠BCD且交AD于点E,A F∥CE,且交BC于点F.
(1)求证:△ABF≌△CDE;
(2)如图,若∠1=65°,求∠B的大小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC为等边三角形,AB=2,点D为边AB上一点,过点D作DE∥AC,交BC于E点;过E点作EF⊥DE,交AB的延长线于F点.设AD=x,△DEF的面积为y,则能大致反映y与x函数关系的图象是( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数
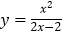 的图象与性质.下面是小文的探究过程,请补充完整:
的图象与性质.下面是小文的探究过程,请补充完整:(1)函数
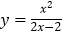 的自变量
的自变量 的取值范围是__________;
的取值范围是__________;(2)下表是
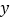 与
与 的几组对应值:
的几组对应值:
如图,在平面直角坐标系
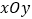 中,描出了以上表中各对应值为坐标的点.
中,描出了以上表中各对应值为坐标的点.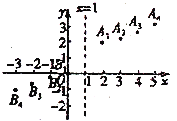
①观察图中各点的位置发现:点
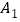 和
和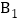 ,
,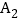 和
和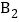 ,
,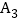 和
和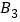 ,
,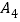 和
和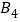 均关于某点中心对称,则该点的坐标为__________;
均关于某点中心对称,则该点的坐标为__________;②小文分析函数
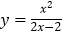 表达式发现:当
表达式发现:当 时,该函数的最大值为0,则该函数图象在直线
时,该函数的最大值为0,则该函数图象在直线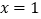 左侧的最高点的坐标为__________;
左侧的最高点的坐标为__________;(3)小文补充了该函数图象上两个点
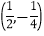 ,
,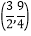 .
.①在上图中描出这两个点,并画出该函数的图象;
②写出该函数的一条性质:__________.
相关试题

