搜索
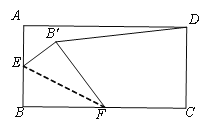
【题目】如图，矩形ABCD中，AD＝4，AB＝2．点E是AB的中点，点F是BC边上的任意一点（不与B、C重合），△EBF沿EF翻折，点B落在B'处，当DB'的长度最小时，BF的长度为________．
参考答案：
【答案】
【解析】
根据题意可知当FB'⊥DE时，DB'的长度最小，则根据勾股定理求出DE=
，设BF=x，根据折叠的性质可得B’E=1, B’F=x,则DB'=-1，FC=4-x,再根据DF是两个直角三角形的斜边，可根据勾股定理列出方程即可求解.
如图，当FB'⊥DE时，DB'的长度最小，
∵点E是AB的中点，
∴AE=BE=
=1
∴DE=
设BF=x，
∵折叠，∴B’E=1, B’F=x,
故DB'=-1，FC=4-x,
在Rt△DCF和Rt△B’DF中，
DF2=
即
解得x=
即BF=
故填：.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线
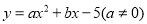经过x轴上的点A（1，0）和点B及y轴上的点C，经过B、C两点的直线为
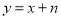．①求抛物线的解析式．
②点P从A出发，在线段AB上以每秒1个单位的速度向B运动，同时点E从B出发，在线段BC上以每秒2个单位的速度向C运动．当其中一个点到达终点时，另一点也停止运动．设运动时间为t秒，求t为何值时，△PBE的面积最大并求出最大值．
③过点A作
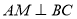于点M，过抛物线上一动点N（不与点B、C重合）作直线AM的平行线交直线BC于点Q．若点A、M、N、Q为顶点的四边形是平行四边形，求点N的横坐标．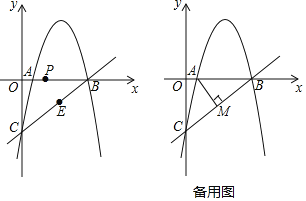
-
科目： 来源： 题型：
查看答案和解析>>【题目】鄂州市化工材料经销公司购进一种化工原料若干千克，价格为每千 克30元．物价部门规定其销售单价不高于每千克60元，不低于每千克30元．经市场调查发现：日销售量y（千克）是销售单价x（元）的一次函数，且当x=60时 ，y=80；x=50时，y=100．在销售过程中，每天还要支付其他费用450元．
（1）（3分）求出y与x的函数关系式，并写出自变量x的取值范围．
（2）（3分）求该公司销售该原料日获利w（元）与销售单价x（元）之间的函数关系式．
（3）（4分）当销售单价为多少元时，该公司日获利最大？最大获利是多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知AB是⊙O的直径，点C在⊙O上，过点C的直线与AB的延长线交于点P，AC=PC，∠COB=2∠PCB.
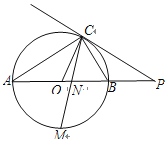
（1）求证：PC是⊙O的切线；
（2）求证：BC=
AB；（3）点M是弧AB的中点，CM交AB于点N，若AB=4，求MN
MC的值. -
科目： 来源： 题型：
查看答案和解析>>【题目】中雅培粹学校举办运动会，全校有3000名同学报名参加校运会，为了解各类运动赛事的分布情况，从中抽取了部分同学进行统计：A.田径类，B.球类，C.团体类，D.其他，并将统计结果绘制成如图所示的两幅不完整的统计图.
（1）这次统计共抽取了 位同学，扇形统计图中的
，
的度数是 ；（2）请将条形统计图补充完整；
（3）估计全校共多少学生参加了球类运动.
-
科目： 来源： 题型：
查看答案和解析>>【题目】吉祥超市准备购进甲、乙两种绿色袋装食品共800袋．甲、乙两种绿色袋装食品的进价和售价如表．已知：用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同．
甲
乙
进价（元/袋）
m
m﹣2
售价（元/袋）
20
13
（1）求m的值；
（2）假如购进的甲、乙两种绿色袋装食品全部卖出，所获总利润不少于5200元，且不超过5280元，问该超市有几种进货方案？（利润＝售价﹣进价）
-
科目： 来源： 题型：
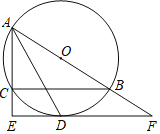
查看答案和解析>>【题目】如图，⊙O是△ABC的外接圆，AB为直径，∠BAC的平分线交⊙O于点D，过点D作DE⊥AC分别交AC的延长线于点E，交AB的延长线于点F．
（1）求证：EF是⊙O的切线；
（2）若AC＝8，CE＝4，求弧BD的长．（结果保留π）
相关试题
