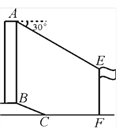
【题目】如图,某学校一教学楼高AB=15米,在它的正前方有一旗杆EF,从教学楼顶端A测得旗杆顶端E的俯角为30°,旗杆低端F到大楼前梯坎底边的距离CF=12米,梯坎坡长BC=6.5米,梯坎坡度i=1:2.4,求旗杆EF的高度.(结果保留根号)
参考答案:
【答案】(17.5-![]() )米.
)米.
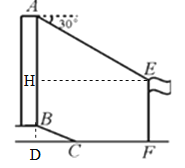
【解析】分析:过点B作BD⊥CF于点D,过点E作EH⊥AB于点H.由梯坎坡度i=1:2.4,BC=6.5米,得到BD、CD的长,进而得到DF的长.解Rt△AEH中,得到AH的长,从而得到BH的长,由EF=DH=即可得出结论.
详解:过点B作BD⊥CF于点D,过点E作EH⊥AB于点H.
在Rt△BCD中,tan∠BCD=![]() ,BC=6.5米,∴BD=2.5米,CD=6米,
,BC=6.5米,∴BD=2.5米,CD=6米,
∴DF=EH=18米.
在Rt△AEH中,tan30°=![]() =
=![]() ,∴AH=6
,∴AH=6![]() 米,
米,
∴BH=![]() 米,
米,
∴EF=DH=(17.5-![]() )米,即旗杆的高度为(17.5-
)米,即旗杆的高度为(17.5-![]() )米.
)米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农户承包荒山若干亩,种果树2000棵.今年水果总产量为18000千克,此水果在市场上每千克售
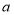 元,在果园每千克售
元,在果园每千克售 元
元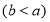 .该农户将水果拉到市场出售平均每天出售1000千克,需8人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元.
.该农户将水果拉到市场出售平均每天出售1000千克,需8人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元.(1)分别用
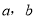 表示两种方式出售水果的收入.
表示两种方式出售水果的收入.(2)若
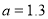 元,
元,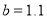 元,且两种方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
元,且两种方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备购进一批A、B两型号节能灯,已知2只A型节能灯和3只B型节能灯共需31元;1只A型节能灯和2只B型节能灯共需19元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元?
(2)学校准备购进这两种型号的节能灯共100只,并且A型节能灯的数量不多于B型节能灯数量的2倍,请设计出最省钱的购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平移和翻折是初中数学两种重要的图形变化.
(1)平移运动
①把笔尖放在数轴的原点处,先向负方向移动3个单位长度,再向正方向移动
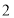 个单位长度,这时笔尖的位置表示什么数?用算式表示以上过程及结果是( )
个单位长度,这时笔尖的位置表示什么数?用算式表示以上过程及结果是( )A.
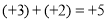 B.
B.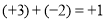
C.
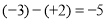 D.
D.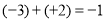
②一机器人从原点O开始,第1次向左跳1个单位,紧接着第2次向右跳2个单位,第3次向左跳3个单位,第4次向右跳4个单位,……,依次规律跳,当它跳2019次时,落在数轴上的点表示的数是_____.
(2)翻折变换
①若折叠纸条,表示-1的点与表示3的点重合,则表示2019的点与表示_______的点重合.
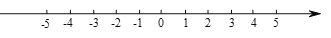
②若数轴上A、B两点之间的距离为2019(A在B的左侧,且折痕与①折痕相同),且A、B两点经折叠后重合,则A点表示_____B点表示______.
③若数轴上折叠重合的两点的数分别为a,b,折叠中间点表示的数为____.(用含有a,b的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AC于点E,交BC于点F,连接BE、DF,且BE平分∠ABD.
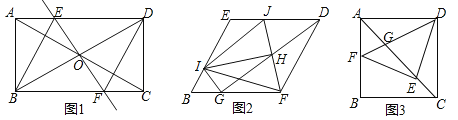
(1)①求证:四边形BFDE是菱形;②求∠EBF的度数.
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的数量关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+b交x轴于点A(1,0),与双曲线y=-
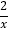 (x<0)交于点B(-1,a).
(x<0)交于点B(-1,a).(1)求直线AB的解析式;
(2)若点B左侧一直线x=m与直线AB交于点C,与双曲线交于点D(C、D两点不重合),当BC=BD时,求m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC和△DEC都是等腰直角三角形,C为它们的公共直角顶点,D、E分别在BC、AC边上.
(1)如图1,F是线段AD上的一点,连接CF,若AF=CF;
①求证:点F是AD的中点;
②判断BE与CF的数量关系和位置关系,并说明理由;
(2)如图2,把△DEC绕点C顺时针旋转α角(0<α<90°),点F是AD的中点,其他条件不变,判断BE与CF的关系是否不变?若不变,请说明理由;若要变,请求出相应的正确结论.

相关试题

