【题目】已知点A,B是数轴上的点,且点A表示数-3,请参照图并思考,完成下列各题:
![]()
(1)将A点向右移动4个单位长度,那么终点B表示的数是 ,此时 A,B两点间的距离是 .
(2)若把数轴绕点A对折,则对折后,点B落在数轴上的位置所表示的数为 .
(3)若(1)中点B以每秒2个单位长度沿数轴向左运动,A不动,多长时间后,点B与点A距离为2个单位长度?试列式计算.
参考答案:
【答案】(1)1,4; (2)-7;(3)或3秒钟后,点B与点A距离为2个单位长度.
【解析】
根据点在数轴上移动法则和点之间距离公式可直接解答此题.
(1)1;4.
(2)-7.
(3)[ 1-(-3)-2]÷2=1, [ 1-(-3)+2]÷2=3,
所以,1或3秒钟后,点B与点A距离为2个单位长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为E.
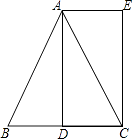
(1)求证:△ABD≌△CAE;
(2)连接DE,线段DE与AB之间有怎样的位置和数量关系?请证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,平面直角坐标系中,A(0,4),B(0,2),点C是x轴上一点,点D为OC的中点.
(1)求证:BD∥AC;
(2)若点C在x轴正半轴上,且BD与AC的距离等于1,求点C的坐标;
(3)如果OE⊥AC于点E,当四边形ABDE为平行四边形时,求直线AC的解析式.
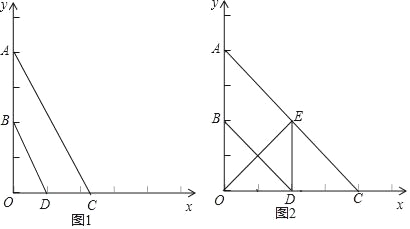
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣2x﹣
 =0的某个根,也是一元二次方程x2﹣(k+2)x+
=0的某个根,也是一元二次方程x2﹣(k+2)x+  =0的根,求k的值.
=0的根,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明在研究性学习活动中,对自己家所在的小区进行调查后发现,小区汽车入口宽AB为3.2m,在入口的一侧安装了停止杆CD,其中AE为支架.当停止杆仰起并与地面成60°角时,停止杆的端点C恰好与地面接触.此时CA为0.7m.在此状态下,若一辆货车高3m,宽2.5m,入口两侧不能通车,那么这辆货车在不碰杆的情况下,能从入口内通过吗?请你通过估算说明.(参考数据:
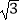 ≈1.7)
≈1.7) 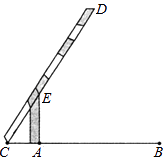
-
科目: 来源: 题型:
查看答案和解析>>【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)小明选择哪家快递公司更省钱?
相关试题

