Question

【题目】如图，已知抛物线y=x2﹣（m+3）x+9的顶点C在x轴正半轴上，一次函数y=x+3与抛物线交于A、B两点，与x、y轴分别交于D、E两点．

（1）求m的值；

（2）求A、B两点的坐标；

（3）当﹣3＜x＜1时，在抛物线上是否存在一点P，使得△PAB的面积是△ABC面积的2倍？若存在，请求出点P的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）m=3；（2）点A的坐标为（1，4），点B的坐标为（6，9）； （3）存在，P（， ）．

【解析】试题分析：（1）由顶点在x轴上知它与x轴只有一个交点，即对应一元二次方程中△=0，可得关于m的方程，求解即可得m；

（2）联立抛物线与直线解析式可得方程组，求解即可得A、B坐标；

（3）设点P（a，b），作PT⊥x轴交BD于点E，AR⊥x轴，BS⊥x轴，分别表示出AR、BS、RC、CS、RS、PT、RT、ST的长，根据S△ABC=S梯形ARSB﹣S△ARC﹣S△BCS求出S△ABC，由S△PAB=S梯形PBST﹣S梯形ABSR﹣S梯形ARTP表示出S△PAB，根据△PAB的面积是△ABC面积的2倍可得a、b间关系，代入抛物线解析式即可求得．

试题解析：（1）∵抛物线的顶点在x轴上，

∴它与x轴只有一个交点，

∴（m+3）2﹣4×9=0，

解得m=3或m=﹣9，

又∵抛物线对称轴大于0

∴﹣＞0，即m＞﹣3，

∴m=3；

（2）由（1）可得抛物的解析式为y=x2﹣6x+9，

解方程组 ，解得或，

∴点A的坐标为（1，4），点B的坐标为（6，9）；

（3）存在，

设点P（a，b），如图，作PT⊥x轴交BD于点E，AR⊥x轴，BS⊥x轴，

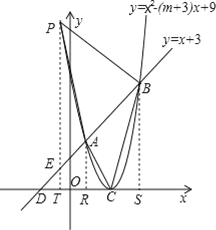
∵A（1，4），B（6，9），C（3，0），P（a，b）

∴AR=4，BS=9，RC=3﹣1=2，CS=6﹣3=3，RS=6﹣1=5，PT=b，RT=1﹣a，ST=6﹣a，

∴S△ABC=S梯形ARSB﹣S△ARC﹣S△BCS=×（4+9）×5﹣×2×4﹣×3×9=15，

S△PAB=S梯形PBST﹣S梯形ABSR﹣S梯形ARTP

=×（9+b）（6﹣a）﹣×（4+9）×5﹣×（b+4）（1﹣a）

=（5b﹣5a﹣15），

又∵S△PAB=2S△ABC，∴（5b﹣5a﹣15）=30，∴b﹣a=15，b=15+a，

∵点P在抛物线上∴b=a2﹣6a+9，∴15+a=a2﹣6a+9，

∴a2﹣7a﹣6=0，解得：a=，

∵﹣3＜a＜1，∴a=，∴b=15+a=，

∴P（， ）．