【题目】如图:在平行四边形ABCD的边AB,CD上截取AF,CE,使得AF=CE,连接EF,点M,N是线段EF上两点,且EM=FN,连接AN,CM.
(1)求证:△AFN≌△CEM;
(2)若∠CMF=107°,∠CEM=72°,求∠NAF的度数.

参考答案:
【答案】(1)证明见解析;(2)∠NAF=35°.
【解析】
(1)利用平行线的性质,根据SAS即可证明;
(2)利用全等三角形的性质可知∠NAF=∠ECM,求出∠ECM即可.
(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB,
∴∠AFN=∠CEM,
∵FN=EM,AF=CE,
∴△AFN≌△CEM(SAS).
(2)解:∵△AFN≌△CEM,
∴∠NAF=∠ECM,
∵∠CMF=∠CEM+∠ECM,
∴107°=72°+∠ECM,
∴∠ECM=35°,
∴∠NAF=35°.
-
科目: 来源: 题型:
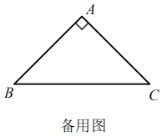
查看答案和解析>>【题目】在RtΔABC中,∠BAC=90°,点O是△ABC所在平面内一点,连接OA,延长OA到点E,使得AE=OA,连接OC,过点B作BD与OC平行,并使∠DBC=∠OCB,且BD=OC,连接DE.
(1)如图一,当点O在RtΔABC内部时.

①按题意补全图形;
②猜想DE与BC的数量关系,并证明.
(2)若AB=AC(如图二),且∠OCB=30°,∠OBC=15°,求∠AED的大小.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,E是BC的中点,连接AE,过点E作EF⊥AE交DC于点F,连接AF.设
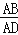 =k,下列结论:(1)△ABE∽△ECF,(2)AE平分∠BAF,(3)当k=1时,△ABE∽△ADF,其中结论正确的是( )
=k,下列结论:(1)△ABE∽△ECF,(2)AE平分∠BAF,(3)当k=1时,△ABE∽△ADF,其中结论正确的是( )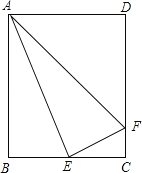
A.(1)(2)(3) B.(1)(3) C.(1)(2) D.(2)(3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】“校园手机”现象越来越受到社会的关注.“五一”期间,小记者刘凯随机调查了城区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如下的统计图:

(1)求这次调查的家长人数,并补全图①;
(2)求图②中表示家长“赞成”的圆心角的度数;
(3)从这次接受调查的学生中,随机抽查一个,恰好是“无所谓”态度的学生的概率是多少?
-
科目: 来源: 题型:
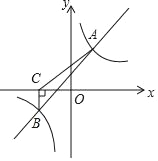
查看答案和解析>>【题目】如图所示,一次函数y=kx+b与反比例函数y=
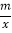 的图象交于A(2,4),B(﹣4,n)两点.
的图象交于A(2,4),B(﹣4,n)两点.(1)分别求出一次函数与反比例函数的表达式;
(2)过点B作BC⊥x轴,垂足为点C,连接AC,求△ACB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】10个人围成一圈做游戏.游戏的规则是:每个人心里都想一个数,并把目己想的数告诉与他相邻的两个人,然后每个人将与他相邻的两个人告诉他的数的平均数报出来,若报出来的数如图所示,则报出来的数是3的人心里想的数是( )

A.2B.
 C.4D.
C.4D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一批电视机,一月份每台毛利润是售出价的20%(毛利润=售出价-买入价),二月份该商场将每台售出价调低10%(买入价不变),结果销售台数比一月份增加120%,那么二月份的毛利润总额与一月份毛利润总额的比是__________。
相关试题

