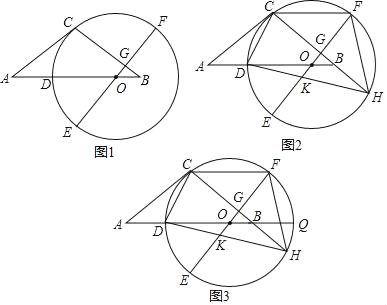
【题目】如图1,等腰△ABC中,AC=BC,点O在AB边上,以O为圆心的圆与AC相切于点C,交AB边于点D,EF为⊙O的直径,EF⊥BC于点G.
(1)求证:D是弧EC的中点;
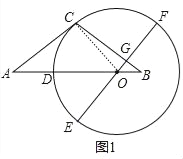
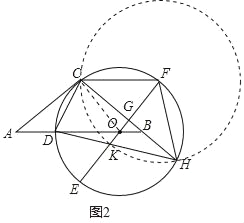
(2)如图2,延长CB交⊙O于点H,连接HD交OE于点K,连接CF,求证:CF=OK+DO;
(3)如图3,在(2)的条件下,延长DB交⊙O于点Q,连接QH,若DO=![]() ,KG=2,求QH.
,KG=2,求QH.
参考答案:
【答案】(1)证明见解析(2)证明见解析(3)![]()
【解析】(1)如图1中,连接OC,根据等角的余角相等,证明即可.
(2)如图2中,连接OC,首先证明,再证明点K在以F为圆心FC为半径的圆上即可解决问题;
(3)如图3中,连接OC、作HM⊥AQ于M.设OK=x,则CF= ![]() ,OG=2-x,GF=
,OG=2-x,GF=![]() ,根据CG2=CF2-FG2=CO2-OG2,列出方程求出x,再想办法求出HM、MQ即可解决问题.
,根据CG2=CF2-FG2=CO2-OG2,列出方程求出x,再想办法求出HM、MQ即可解决问题.
(1)证明:如图1中,连接OC.
∵AC是⊙O的切线,
∴OC⊥AC,
∴∠ACO=90°,
∴∠A+∠AOC=90°,
∵CA=CB,
∴∠A=∠B,
∵EF⊥BC,
∴∠OGB=90°,
∴∠B+∠BOG=90°,
∴∠BOG=∠AOC,
∵∠BOG=∠DOE,
∴∠DOC=∠DOE,
∴点D是![]() 的中点.
的中点.
(2)证明:如图2中,连接OC.
∵EF⊥HC,
∴CG=GH,
∴EF垂直平分HC,
∴FC=FH,
∵∠CFK=![]() ∠COE,
∠COE,
∵∠COD=∠DOE,
∴∠CFK=∠COD,
∵∠CHK=![]() ∠COD,
∠COD,
∴∠CHK=![]() ∠CFK,
∠CFK,
∴点K在以F为圆心FC为半径的圆上,
∴FC=FK=FH,
∵DO=OF,
∴DO+OK=OF+OK=FK=CF,
即CF=OK+DO;
(3)解:如图3中,连接OC、作HM⊥AQ于M.设OK=x,则CF=![]() +x,OG=2﹣x,GF=
+x,OG=2﹣x,GF=![]() ﹣(2﹣x),
﹣(2﹣x),

∵CG2=CF2﹣FG2=CO2﹣OG2,
∴(![]() +x)2﹣[
+x)2﹣[![]() (2﹣x)]2=(
(2﹣x)]2=(![]() )2﹣(2﹣x)2,
)2﹣(2﹣x)2,
解得x=![]() ,
,
∴CF=5,FG=4,CG=3,OG=![]() ,
,
∵∠CFE=∠BOG,
∴CF∥OB,
∴![]() =
=![]() =
=![]() ,
,
可得OB=![]() ,BG=
,BG=![]() ,BH=
,BH=![]() ,
,
由△BHM∽△BOG,可得![]() =
=![]() =
=![]() ,
,
∴BM=![]() ,HM=
,HM=![]() ,MQ=OQ﹣OB﹣BM=
,MQ=OQ﹣OB﹣BM=![]() ,
,
在Rt△HMQ中,QH=![]() =
=![]() =
=![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】淮安日报社为了了解市民“获取新闻的主要途径”,开展了一次抽样调查,根据调查结果绘制了如图三种不完整的统计图表.

请根据图表信息解答下列问题:
(1)统计表中的m= ,n= ;
(2)并请补全条形统计图;
(3)若该市约有80万人,请你估计其中将“电脑上网”和“手机上网”作为“获取新闻的主要途径”的总人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.

(1)求证:四边形AMDN是平行四边形.
(2)当AM的值为何值时,四边形AMDN是矩形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 与x轴交点A(1,0),B(-3,0) .与y轴交点B(0,3),如图1所示,D为抛物线的顶点。
与x轴交点A(1,0),B(-3,0) .与y轴交点B(0,3),如图1所示,D为抛物线的顶点。(1)求抛物线的解析式;
(2)如图1若R为y轴上的一个动点,连接AR,则

 RB+AR的最小值为
RB+AR的最小值为 (3)在x轴上取一动点P(m,0),
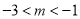 ,过点P作x轴的垂线,分别交抛物线、CD、CB于点Q、F、E,如图2所示,求证EF=EP.
,过点P作x轴的垂线,分别交抛物线、CD、CB于点Q、F、E,如图2所示,求证EF=EP.(4)设此抛物线的对称轴为直线MN,在直线MN上取一点T,使∠BTN=∠CTN.直接写出点T的坐标。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点,作△ABC的外接圆⊙O,则弧AC的长等于( )
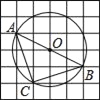
A. π B.
 C.
C. 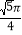 D.
D. 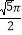
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的面积为32,点D在线段AC上,点F在线段BC的延长线上,且BC=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )

A. 8 B. 6 C. 4 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动,它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.例如从A到B记为:A →B(+1,+3),从B到A记为:B→A(﹣1,-3),其中第一个数表示左右方向,第二个数表示上下方向.


(1)图中A →C(______,______),B →C(______,______),C→_______(+1,﹣2);
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(3)从A处去P处的行走路线依次为(+2,+2),(+2,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出P的位置;
(4)若图中另有两个格点M、N,且M→A(3-a,b-4),M→N(5-a,b-2),则N→A应记为什么?
相关试题

