搜索
【题目】若|x|=3，|y|=4，且|x﹣y|=y﹣x，则xy的值为（ ）
A.﹣1
B.﹣12
C.12
D.12或﹣12
参考答案：
【答案】D
【解析】解：∵|x|=3，|y|=4，且|x﹣y|=y﹣x，
∴x=﹣3，y=4；x=3，y=4，
则xy=﹣12或12，
故选D
【考点精析】解答此题的关键在于理解有理数的减法的相关知识，掌握有理数减法法则：减去一个数，等于加上这个数的相反数；即a-b=a+（-b），以及对有理数的乘法法则的理解，了解有理数乘法法则：1、两数相乘，同号为正，异号为负，并把绝对值相乘2、任何数同零相乘都得零3、几个数相乘，有一个因式为零，积为零；各个因式都不为零，积的符号由负因式的个数决定．
-
科目： 来源： 题型：
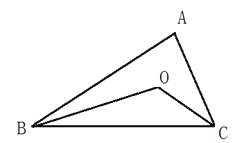
查看答案和解析>>【题目】（本题共10分）AB和AC 相交于点A， BD和CD相交于点D，探究∠BDC与∠B 、 ∠C、∠BAC的关系．
小明是这样做的：
解：以点A为端点作射线AD．
∵∠1是△ABD的外角，∴∠1= ∠B+∠BAD．
同理∠2=∠C+∠CAD．
∴∠1+∠2=∠B+∠BAD+∠C+∠CAD．即∠BDC=∠B+∠C+∠BAC．
小英的思路是：延长BD交AC于点E．
（1）按小英的思路完成∠BDC=∠B+∠C+∠BAC这一结论．
（2）按照上面的思路解决如下问题：如图：在△ABC中，BE、CD分别是∠ABC∠ACB的角平分线，交AC于E，交AB于D．BE、CD相交于点O，∠A=60°．求∠BOC的度数．
（3）如图：△ABC中，BO、CO分别是∠ABC与∠ACB的角平分线，且BO、CO相交于点O．猜想∠BOC与∠A有怎样的关系，并加以证明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】有这样一个问题：探究函数
的图象与性质．小东根据学习函数的经验，对函数
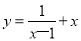的图象与性质进行了探究．下面是小东的探究过程，请补充完整：
（1） 函数
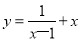的自变量x的取值范围是___________；（2）下表是y与x的几组对应值．
x
…
－3
－2
－1
0
2
3
4
5
…
y
…
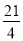
3
m
…
求m的值；
（3） 如图，在平面直角坐标系
中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；
（4）进一步探究发现，该函数图象在第一象限内的最低点的坐标是(2，3)，结合函数的图象，写出该函数的其它性质（一条即可）：
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明爸爸经营的水果店出售一种优质热带水果，正在上初三的小明经过调查和计算，发现这种水果每月的销售量y(千克)与销售单价x（元）之间存在着一次函数关系：y=-10x+500(20≤x≤50)．下面是他们的一次对话：
小明：“您要是告诉我咱家这种水果的进价是多少？我就能帮你预测好多信息呢！”
爸爸：“咱家这种水果的进价是每千克20元”
聪明的你，也来解答一下小明想要解决的两个问题：
（1）若每月获得利润w(元）是销售单价x（元）的函数，求这个函数的表达式．
（2）当销售单价为多少元时，每月可获得最大利润？
-
科目： 来源： 题型：
查看答案和解析>>【题目】若a＜0，b＜0，则下列各式正确的是（ ）
A.a﹣b＜0
B.a﹣b＞0
C.a﹣b=0
D.ab＞0 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知关于x的方程
（1）求证：无论
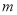取任何实数时，方程恒有实数根；（2）若关于
的二次函数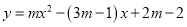
的图象与
轴两个交点的横坐标均为整数，求m的整数值. -
科目： 来源： 题型：
查看答案和解析>>【题目】下列运算正确的是（ ）
A.x3x2=x5
B.（x3）3=x6
C.x5+x5=x10
D.x6﹣x3=x3
相关试题
