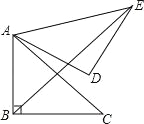
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC=![]() ,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BE,则BE的长是 .
,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BE,则BE的长是 .
参考答案:
【答案】2+2![]()
【解析】
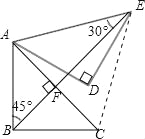
试题分析:首先考虑到BE所在的三角形并不是特殊三角形,所以猜想到要求BE,可能需要构造直角三角形.由旋转的性质可知,AC=AE,∠CAE=60°,故△ACE是等边三角形,设BE与AC相交于点F,如下图所示,可证明△ABE与△CBE全等,可得到∠ABE=45°,∠AEB=30°,再证△AFB和△AFE是直角三角形,然后在△ABF中,∠BFA=180°﹣45°﹣45°=90°可得∠AFB=∠AFE=90°在Rt△ABF中,由勾股定理得,BF=AF=![]() =2,又在Rt△AFE中,∠AEF=30,°∠AFE=90°,FE=
=2,又在Rt△AFE中,∠AEF=30,°∠AFE=90°,FE=![]() AF=2
AF=2![]() ,BE=BF+FE=2+2
,BE=BF+FE=2+2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若﹣7xm+2y与﹣3x3yn是同类项,则m= , n= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将菱形纸片AB(E)CD(F)沿对角线BD(EF)剪开,得到△ABD和△ECF,固定△ABD,并把△ABD与△ECF叠放在一起.
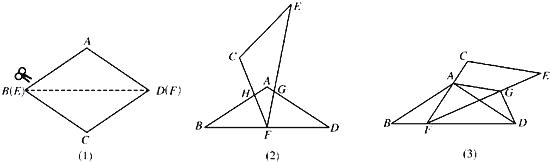
(1)操作:如图2,将△ECF的顶点F固定在△ABD的BD边上的中点处,△ECF绕点F在BD边上方左右旋转,设旋转时FC交BA于点H(H点不与B点重合),FE交DA于点G(G点不与D点重合).
求证:BHGD=BF2
(2)操作:如图3,△ECF的顶点F在△ABD的BD边上滑动(F点不与B、D点重合),且CF始终经过点A,过点A作AG∥CE,交FE于点G,连接DG.
探究:FD+DG= .请予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,山坡AB的坡度i=1:
 ,AB=10米,AE=15米.在高楼的顶端竖立一块倒计时牌CD,在点B处测量计时牌的顶端C的仰角是45°,在点A处测量计时牌的底端D的仰角是60°,求这块倒计时牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:
,AB=10米,AE=15米.在高楼的顶端竖立一块倒计时牌CD,在点B处测量计时牌的顶端C的仰角是45°,在点A处测量计时牌的底端D的仰角是60°,求这块倒计时牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据: ≈1.414,
≈1.414,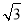 ≈1.732)
≈1.732)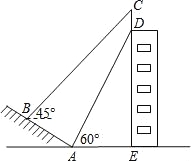
-
科目: 来源: 题型:
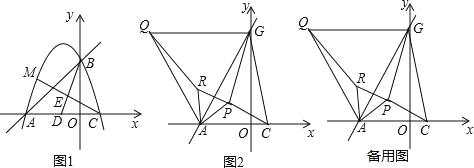
查看答案和解析>>【题目】如图1,已知一次函数y=x+3的图象与x轴、y轴分别交于A、B两点,抛物线y=﹣x2+bx+c过A、B两点,且与x轴交于另一点C.
(1)求b、c的值;
(2)如图1,点D为AC的中点,点E在线段BD上,且BE=2ED,连接CE并延长交抛物线于点M,求点M的坐标;
(3)将直线AB绕点A按逆时针方向旋转15°后交y轴于点G,连接CG,如图2,P为△ACG内一点,连接PA、PC、PG,分别以AP、AG为边,在他们的左侧作等边△APR,等边△AGQ,连接QR
①求证:PG=RQ;
②求PA+PC+PG的最小值,并求出当PA+PC+PG取得最小值时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】比较大小:﹣(﹣5)2﹣|﹣62|.
-
科目: 来源: 题型:
查看答案和解析>>【题目】疫情期间,某地向武汉捐赠口罩1200000只,其中数1200000用科学记数法表示是( )
A.12×105B.12×106C.1.2×105D.1.2×106
相关试题

