【题目】如图有一座抛物线形拱桥，桥下面在正常水位是AB宽20m，水位上升3m就达到警戒线CD，这是水面宽度为10m。

（1）在如图的坐标系中求抛物线的解析式。

(2)若洪水到来时，水位以每小时0.2m的速度上升，从警戒线开始，再持续多少小时才能到拱桥顶？

参考答案：

【答案】5小时

【解析】试题分析：（1）首先设所求抛物线的解析式为：y=ax2（a≠0），再根据题意得到C（-5，-1），利用待定系数法即可得到抛物线解析式；

（2）根据抛物线解析式计算出A点坐标，进而得到F点坐标，然后计算出EF的长，再算出持续时间即可．

试题解析：（1）设所求抛物线的解析式为：y=ax2（a≠0），

∵由CD=10m，CD到拱桥顶E的距离仅为1m，

则C（-5，-1），

把C的坐标分别代入y=ax2得：a=-，

故抛物线的解析式为y=-x2；

（2）如图：

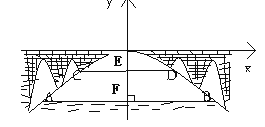
∵AB宽20m，

∴设A（-10，b），

把A点坐标代入抛物线的解析式为y=-x2中，

解得：b=-4，

∴F（0，-4），

∴EF=3，

∵水位以每小时0.3m的速度上升，

∴3÷0.3=10（小时），

答：从正常水位开始，持续10小时到达警戒线．

关闭