【题目】如图,长方形ABCD中,AB=6,BC=8,点P从A出发沿A→B→C→D的路线移动,设点P移动的路线为x,△PAD的面积为y.
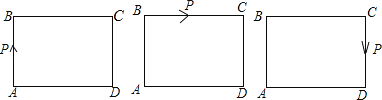
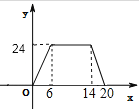
(1)写出y与x之间的函数关系式,并在坐标系中画出这个函数的图象.
(2)求当x=4和x=18时的函数值.
(3)当x取何值时,y=20,并说明此时点P在长方形的哪条边上.
参考答案:
【答案】(1)y与x之间的函数关系式为y=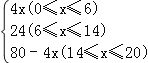 ;
;
(2)当x=4时,y=4x=4×4=16,当x=18时,y=80﹣4x=80﹣4×18=8;
(3)当y=4x=20,解得x=5,此时点P在线段AB上,
当y=80﹣4x=20,解得x=15,此时点P在线段CD上.
【解析】
试题分析:(1)分点P在线段AB上运动时、点P在线段BC上运动时和点P在线段CD上运动时三种情况;
(2)分别将x=4和x=18代入上题求得的函数关系式即可求得其面积;
(3)令y=20,求得x的值,然后根据x的值的大小确定点P的位置即可.
解:(1)当点P在线段AB上时,
此时AP=x,AD=8,
根据三角形的面积公式可得:y=![]() ADAP=
ADAP=![]() ×8×x=4x,
×8×x=4x,
当点P在线段BC上运动时,面积不变;
当点P在线段CD上运动时,
DP=6+8+6﹣x=20﹣x,AD=8
根据三角形的面积公式可得:y=![]() ADDP=
ADDP=![]() ×8×(20﹣x)=80﹣4x,
×8×(20﹣x)=80﹣4x,
∴y与x之间的函数关系式为y=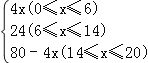
(2)当x=4时,y=4x=4×4=16,
当x=18时,y=80﹣4x=80﹣4×18=8;
(3)当y=4x=20,解得x=5,此时点P在线段AB上,
当y=80﹣4x=20,解得x=15,此时点P在线段CD上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点O是AC边上的一动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
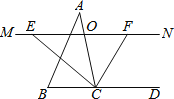
(1)求证:EO=FO;
(2)当O点运动到何处时,四边形AECF是矩形?并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将x1=
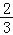 代入反比例函数y=﹣
代入反比例函数y=﹣ 中,所得的函数值记为y1,将x2=y1+1代入反比例函数y=﹣
中,所得的函数值记为y1,将x2=y1+1代入反比例函数y=﹣ 中,所得的函数值记为y2,再将x3=y2+1代入函数y=﹣
中,所得的函数值记为y2,再将x3=y2+1代入函数y=﹣ 中,所得的函数值记为y3…,将xn=y(n﹣1)+1 代入反比例函数y=﹣
中,所得的函数值记为y3…,将xn=y(n﹣1)+1 代入反比例函数y=﹣ 中,所得的函数值记为yn (其中n≥2,且n是整数) 如此继续下去,则在2006个函数值y1.y2,…,y2006中,值为2的情况共出现了 次?
中,所得的函数值记为yn (其中n≥2,且n是整数) 如此继续下去,则在2006个函数值y1.y2,…,y2006中,值为2的情况共出现了 次? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1+∠2=180,∠A=∠C,DA平分∠BDF。
(1)求证:AE∥FC.
(2)AD与BC的位置关系如何,为什么?
(3)证明:BC平分∠DBE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各数中,比﹣1小的数是( )
A、0B、﹣2
C、D、1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数的图象经过点A(2,1),B(﹣1,﹣3).
(1)求此一次函数的解析式;
(2)求此一次函数的图象与x轴、y轴的交点坐标;
(3)求此一次函数的图象与两坐标轴所围成的三角形面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图②的形状拼成一个正方形.
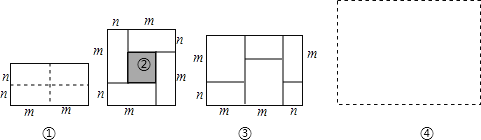
(1)请用两种不同的方法求图②中阴影部分的面积.
方法1:
方法2:
请你写出下列三个代数式:
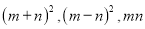 之间的等量关系.
之间的等量关系. ;
(2)根据(1)题中的等量关系,解决如下问题:
已知:
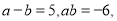 则
则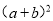 =
= (3)实际上有许多代数恒等式可以用图形的面积来表示.如图③,它表示的代数恒等式是___ .
(4)已知等式:
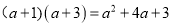 ,请你在图④中画出一个相应的几何图形。
,请你在图④中画出一个相应的几何图形。
相关试题

