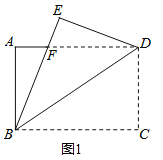
【题目】如图1,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.
(1)求证:BF=DF;
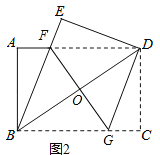
(2)如图2,过点D作DG∥BE,交BC于点G,连结FG交BD于点O.
①求证:四边形BFDG是菱形;
②若AB=3,AD=4,求FG的长.
参考答案:
【答案】(1)见解析;(2)①见解析;②![]() .
.
【解析】
(1)根据两直线平行内错角相等及折叠特性判断;(2)①根据已知矩形性质及第一问证得邻边相等判断;②根据折叠性质设未知边,构造勾股定理列方程求解.
(1)证明:如图1,根据折叠,∠DBC=∠DBE,
又AD∥BC,
∴∠DBC=∠ADB,
∴∠DBE=∠ADB,
∴DF=BF;
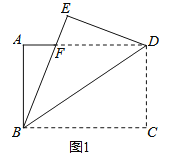
(2)①∵四边形ABCD是矩形,
∴AD∥BC,
∴FD∥BG,
又∵DG∥BE,
∴四边形BFDG是平行四边形,
∵DF=BF,
∴四边形BFDG是菱形;
②∵AB=3,AD=4,
∴BD=5.
∴OB=![]() BD=
BD=![]() .
.
假设DF=BF=x,∴AF=AD-DF=4-x.
∴在直角△ABF中,AB2+AF2=BF2,即32+(4-x)2=x2,
解得x=![]() ,
,
即BF=![]() ,
,
∴由勾股定理得,FO=![]() ,
,
∴FG=2FO=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在海上观察所A,我边防海警发现正北5km的B处有一可疑船只正在向东方向12km的C处行驶.我边防海警即刻派船前往C处拦截.若可疑船只的行驶速度为60km/h,则我边防海警船的速度为多少时,才能恰好在C处将可疑船只截住?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,且抛物线经过A(﹣1,0),C(0,﹣5)两点,与x轴交于点B.

(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)设点P为抛物线上的一个动点,连接PB、PC,若△BPC是以BC为直角边的直角三角形,求此时点P的坐标;
(3)在抛物线上BC段有另一个动点Q,以点Q为圆心作⊙Q,使得⊙Q与直线BC相切,在运动的过程中是否存在一个最大⊙Q?若存在,请直接写出最大⊙Q的半径;若不存在,请说明理由. -
科目: 来源: 题型:
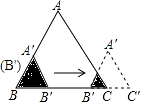
查看答案和解析>>【题目】如图,边长分别为2和4的两个全等三角形,开始它们在左边重叠,大△ABC固定不动,然后把小△A′B′C′自左向右平移,直至移到点B′到C重合时停止,设小三角形移动的距离为x,两个三角形的重合部分的面积为y,则y关于x的函数图象是( )
A.
B.
C.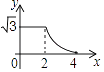
D.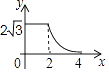
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论是 . (写出正确命题的序号)
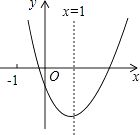
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的图象过P(1,4),Q(4,1)两点,且与x轴交于A点.
(1)求此一次函数的解析式;
(2)求△POQ的面积;
(3)已知点M在x轴上,若使MP+MQ的值最小,
求点M的坐标及MP+MQ的最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰△ABC中,∠A=36°,∠ABC=∠ACB,∠1=∠2,∠3=∠4,BD与CE交于点O,则图中等腰三角形有( )

A. 6个 B. 7个 C. 8个 D. 9个
相关试题

