【题目】如图,在△ABC中,∠B=90°,tan∠C= ![]() ,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
A.18cm2
B.12cm2
C.9cm2
D.3cm2
参考答案:
【答案】C
【解析】解:∵tan∠C= ![]() ,AB=6cm,
,AB=6cm,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴BC=8,
由题意得:AP=t,BP=6﹣t,BQ=2t,
设△PBQ的面积为S,
则S= ![]() ×BP×BQ=
×BP×BQ= ![]() ×2t×(6﹣t),
×2t×(6﹣t),
S=﹣t2+6t=﹣(t2﹣6t+9﹣9)=﹣(t﹣3)2+9,
P:0≤t≤6,Q:0≤t≤4,
∴当t=3时,S有最大值为9,
即当t=3时,△PBQ的最大面积为9cm2;
故选C.
先根据已知求边长BC,再根据点P和Q的速度表示BP和BQ的长,设△PBQ的面积为S,利用直角三角形的面积公式列关于S与t的函数关系式,并求最值即可本题考查了有关于直角三角形的动点型问题,考查了解直角三角形的有关知识和二次函数的最值问题,解决此类问题的关键是正确表示两动点的路程(路程=时间×速度);这类动点型问题一般情况都是求三角形面积或四边形面积的最值问题,转化为函数求最值问题,直接利用面积公式或求和、求差表示面积的方法求出函数的解析式,再根据函数图象确定最值,要注意时间的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:
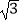 ,则大楼AB的高度约为( )(精确到0.1米,参考数据:
,则大楼AB的高度约为( )(精确到0.1米,参考数据: 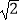 ≈1.41,
≈1.41, 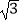 ≈1.73,
≈1.73,  ≈2.45)
≈2.45)
A.30.6
B.32.1
C.37.9
D.39.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】聊城“水城之眼”摩天轮是亚洲三大摩天轮之一,也是全球首座建筑与摩天轮相结合的城市地标,如图,点O是摩天轮的圆心,长为110米的AB是其垂直地面的直径,小莹在地面C点处利用测角仪测得摩天轮的最高点A的仰角为33°,测得圆心O的仰角为21°,则小莹所在C点到直径AB所在直线的距离约为(tan33°≈0.65,tan21°≈0.38)( )

A.169米
B.204米
C.240米
D.407米 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在Rt△ABC中,∠ABC=90°,点D沿BC自B向C运动(点D与点B、C不重合),作BE⊥AD于E,CF⊥AD于F,则BE+CF的值( )

A.不变
B.增大
C.减小
D.先变大再变小 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC.若∠BAC与∠BOC互补,则弦BC的长为( )

A.3
B.4
C.5
D.6
-
科目: 来源: 题型:
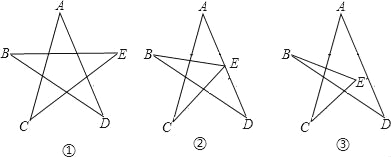
查看答案和解析>>【题目】如图①所示,为五角星图案,图②、图③叫做蜕变的五角星.试回答以下问
(1)在图①中,试证明∠A+∠B+∠C+∠D+∠E=180°;
(2)对于图②或图③,还能得到同样的结论吗?若能,请在图②或图③中任选其一证明你的发现;若不能,试说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,将这条抛物线的顶点记为C,连接AC、BC,则tan∠CAB的值为( )
A.
B.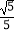
C.
D.2
相关试题

