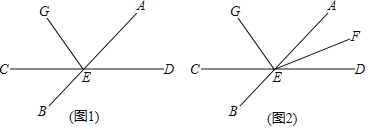
【题目】如图,直线AB与CD相交于点E,射线EG在∠AEC内(如图1).
(1)若∠BEC的补角是它的余角的3倍,则∠BEC= °;
(2)在(1)的条件下,若∠CEG比∠AEG小25度,求∠AEG的大小;
(3)若射线EF平分∠AED,∠FEG=m°(m>90°)(如图2),则∠AEG﹣∠CEG= °(用m的代表式表示).
参考答案:
【答案】(1)45°;(2)∠AEG=80°;(3)2m﹣180
【解析】
(1)设∠BEC=x°,根据题意,可列方程:180﹣x=3(90﹣x),解出∠BEC;
(2)由∠CEG=∠AEG﹣25°,得∠AEG=180°﹣∠BEC﹣∠CEG=180°﹣45°﹣(∠AEG﹣25°),解出∠AEG;
(3)计算出∠AEG和∠CEG,然后相减,即可得到结果.
解:(1)设∠BEC=x°,
根据题意,可列方程:180﹣x=3(90﹣x),
解得x=45°,
故∠BEC=45°,
故答案为:45°;
(2)∵∠CEG=∠AEG﹣25°,
∴∠AEG=180°﹣∠BEC﹣∠CEG
=180°﹣45°﹣(∠AEG﹣25°)=160°﹣∠AEG,
∴∠AEG=80°;
(3)∵EF平分∠AED,
∴∠AEF=∠DEF,
设∠AEF=∠DEF=α,∠AEG=∠FEG﹣∠AEF=m﹣α,
∠CEG=180°﹣∠GEF﹣DEF=180﹣m﹣α,
∴∠AEG﹣∠CEG=m﹣α﹣(180﹣m﹣α)=2m﹣180.
故答案为:2m﹣180.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠A
 90°,AB
90°,AB AC.
AC.(1)如图1,△ABC的角平分线BD,CE交于点Q,请判断“
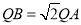 ”是否正确:________(填“是”或“否”);
”是否正确:________(填“是”或“否”);(2)点P是△ABC所在平面内的一点,连接PA,PB,且PB

 PA.
PA.①如图2,点P在△ABC内,∠ABP
 30°,求∠PAB的大小;
30°,求∠PAB的大小;②如图3,点P在△ABC外,连接PC,设∠APC
 α,∠BPC
α,∠BPC β,用等式表示α,β之间的数量关系,并证明你的结论.
β,用等式表示α,β之间的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织部分师生从学校(A地)到300千米外的B地进行红色之旅(革命传统教育),租用了客运公司甲、乙两辆车,其中乙车速度是甲车速度的
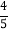 ,两车同时从学校出发,以各自的速度匀速行驶,行驶2小时后甲车到达服务区C地,此时两车相距40千米,甲车在服务区休息15分钟户按原速度开往B地,乙车行驶过程中未做停留.
,两车同时从学校出发,以各自的速度匀速行驶,行驶2小时后甲车到达服务区C地,此时两车相距40千米,甲车在服务区休息15分钟户按原速度开往B地,乙车行驶过程中未做停留.(1)求甲、乙两车的速度?
(2)问甲车在C地结束休息后再行驶多长时间,甲、乙两车相距30千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.

(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
-
科目: 来源: 题型:
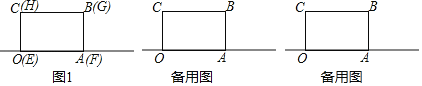
查看答案和解析>>【题目】有两个大小完全一样的长方形OABC和EFGH重合放在一起,边OA、EF在数轴上,O为数轴原点(如图1),长方形OABC的边长OA的长为6个坐标单位.
(1)数轴上点A表示的数为 .
(2)将长方形EFGH沿数轴所在直线水平移动
①若移动后的长方形EFGH与长方形OABC重叠部分的面积恰好等于长方形OABC面积的
 ,则移动后点F在数轴上表示的数为 .
,则移动后点F在数轴上表示的数为 .②若出行EFGH向左水平移动后,D为线段AF的中点,求当长方形EFGH移动距离x为何值时,D、E两点在数轴上表示的数是互为相反数?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场出售一批进价为2元的贺卡,在市场营销中发现此商品的日销售单价x(元)与日销售量y(个)之间有如下关系:
日销售单价x(元)
3
4
5
6
日销售量y(个)
20
15
12
10
(1)猜测并确定y与x之间的函数关系式,并画出图象;
(2)设经营此贺卡的销售利润为W元,求出W与x之间的函数关系式,
(3)若物价局规定此贺卡的售价最高不能超过10元/个,请你求出当日销售单价x定为多少时,才能获得最大日销售利润?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个少年在绿茵场上游戏.小红从点A出发沿线段AB运动到点B,小兰从点C出发,以相同的速度沿⊙O逆时针运动一周回到点C,两人的运动路线如图1所示,其中AC
 DB.两人同时开始运动,直到都停止运动时游戏结束,其间他们与点C的距离y与时间x(单位:秒)的对应关系如图2所示.则下列说法正确的是( )
DB.两人同时开始运动,直到都停止运动时游戏结束,其间他们与点C的距离y与时间x(单位:秒)的对应关系如图2所示.则下列说法正确的是( )

A. 小红的运动路程比小兰的长
B. 两人分别在1.09秒和7.49秒的时刻相遇
C. 当小红运动到点D的时候,小兰已经经过了点D
D. 在4.84秒时,两人的距离正好等于⊙O的半径
相关试题

