Question

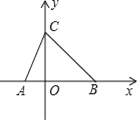
【题目】如图，点A为x轴负半轴上一点，点B为x轴正半轴上一点，OA、OB（OA＜0B）的长分别是关于x的一元二次方程x2﹣4mx+m2+2=0的两根，C（0，3），且△ABC的面积为6，求∠ABC的度数．

Answer 1

【答案】∠ABC=45°．

【解析】试题分析：先根据三角形ABC的面积求出AB的值，再由根与系数的关系就可以求出m的值，从而求出方程的解，就可以得出OB的值，进而得出△OBC为等腰直角三角形就可以得出结论．

试题解析：∵C（0，3），

∴CO=3．

∵△ABC的面积为6，

∴=6，∴AB=4，

∵OA、OB（OA＜0B）的长分别是关于x的一元二次方程x2﹣4mx+m2+2=0的两根，

∴OA+OB=4m，∴4m=4，∴m=1，

∴一元二次方程为：x2﹣4x+3=0，∴x1=1，x2=3，

∵OA＜0B，∴OA=1，OB=3．∴OB=OC，

∴△OBC是等腰直角三角形，

∴∠ABC=45°，

答：∠ABC=45°．