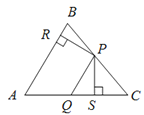
【题目】如图，在△ABC中，点P、Q分别是BC、AC边上的点，PSAC，PRAB，若AQPQ，PRPS，则下列结论：①ASAR；②QP∥AR；③△BRP ≌△CPS；④S四边形ARPQ=．其中正确的结论有____________（填序号）.

参考答案：

【答案】①②

【解析】连接AP.

∵PR=PS，AP=AP，PR⊥AB，PS⊥AC，

∴△APR≌△APS，

∴AS=AR，①正确.

∵PR=PS，PR⊥AB，PS⊥AC，

∴AP是∠BAC的平分线，

∴∠BAP=∠QAP.

∵AQ=PQ，

∴∠QAP=∠QPA，

∴∠BAP=∠QPA，

∴QP∥AR，②正确.

点P是BC的上的点，并没有固定，明显△BRP≌△CSP不成立，故③不正确;

∵

根据已知条件不能得出AR+AQ= (AB+AC)，故④错误；故答案为：①②.

关闭