【题目】已知:梯形![]() 中,
中,![]() ,联结
,联结![]() (如图1). 点
(如图1). 点![]() 沿梯形的边从点
沿梯形的边从点![]() 移动,设点
移动,设点![]() 移动的距离为
移动的距离为![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)当点![]() 从点
从点![]() 移动到点
移动到点![]() 时,
时,![]() 与
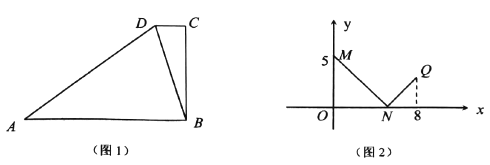
与![]() 的函数关系(如图2)中的折线
的函数关系(如图2)中的折线![]() 所示. 试求
所示. 试求![]() 的长;
的长;
(3)在(2)的情况下,点![]() 从点
从点![]() 移动的过程中,
移动的过程中,![]() 是否可能为等腰三角形?若能,请求出所有能使
是否可能为等腰三角形?若能,请求出所有能使![]() 为等腰三角形的
为等腰三角形的![]() 的取值;若不能,请说明理由.
的取值;若不能,请说明理由.
参考答案:
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 或
或![]()
【解析】
(1)由平行线的性质、直角三角形的性质、等腰三角形的性质得出∠ABD=∠CDB,∠A+∠ADC=180°,∠ABD+∠CBD=90°,∠ABD=∠ADB,得出∠A+2∠ABD=180°,2∠ABD+2∠CBD=180°,即可得出结论;
(2)作DE⊥AB于E,则DE=BC=3,CD=BE,由勾股定理求出AE=![]() =4,得出CD=BE=AB-AE=1;
=4,得出CD=BE=AB-AE=1;
(3)分情况讨论:①点P在AB边上时;②点P在BC上时;③点P在AD上时;由等腰三角形的性质和勾股定理即可得出答案.
(1)证明:∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ,即
,即![]()
∴![]()
(2)解:由点![]() ,得
,得![]() ,
,
由点![]() 点的横坐标是8,得
点的横坐标是8,得![]() 时,∴
时,∴![]()
作![]() 于
于![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]()
(3)
情况一:点![]() 在
在![]() 边上,作
边上,作![]() ,
,
当![]() 时,
时,![]() 是等腰三角形,此时,
是等腰三角形,此时,![]() ,
,
∴![]()
情况二:点![]() 在
在![]() 边上,当
边上,当![]() 时
时![]() 是等腰三角形,
是等腰三角形,
此时,![]() ,
,![]() ,
,
∴在![]() 中,
中,![]() ,
,
即![]() ,
,
∴![]()
情况三:点![]() 在
在![]() 边上时,
边上时,![]() 不可能为等腰三角形
不可能为等腰三角形
情况四:点![]() 在
在![]() 边上,有三种情况
边上,有三种情况
1°作![]() ,当
,当![]() 时,
时,![]() 为等腰三角形,
为等腰三角形,
此时,∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]()
2°当![]() 时
时![]() 为等腰三角形,
为等腰三角形,
此时,![]()
3°当点![]() 与点
与点![]() 重合时
重合时![]() 为等腰三角形,
为等腰三角形,
此时![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入相应的集合.
-17,6.8,+48,0,
 ,-7.9,-π,-5,-
,-7.9,-π,-5,- ,
, ,29,-20%
,29,-20%正数集合:{________________________________…};
负分数集合:{________________________________…};
整数集合:{________________________________…}.
非负整数集合{________________________________…}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为6,B是数轴上在A左侧的一点,且A,B两点间的距离为10.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动。

(1)运动1秒时,数轴上点B表示的数是______点P表示的数是______;
(2)动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动,若点P、Q时出发.求:
①当点P运动多少秒时,点P与点Q相遇?
②当点P运动多少秒时,点P与点Q间的距离为8个单位长度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
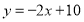 与
与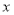 轴交于点
轴交于点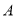 ,点
,点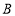 是该直线上一点,满足
是该直线上一点,满足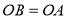 .
. (1)求点
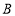 的坐标;
的坐标;(2)若点
 是直线上另外一点,满足
是直线上另外一点,满足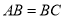 ,且四边形
,且四边形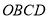 是平行四边形,试画出符合要求的大致图形,并求出点
是平行四边形,试画出符合要求的大致图形,并求出点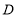 的坐标.
的坐标. 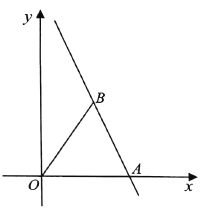
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,AB=AC,∠BAC=90°,BE⊥CE,垂足是E,BE交AC于点D,F是BE上一点,AF⊥AE,且C是线段AF的垂直平分线上的点,AF=2
 ,则DF=______.
,则DF=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们规定:解方程就是求出使方程中等号左右两边相等的未知数的值,这个值就是方程的解(solution).已知:关于
 的方程
的方程 .
.(1)若
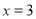 是方程
是方程 的解,求
的解,求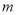 的值;
的值;(2)若关于
 的方程
的方程 的解比方程
的解比方程 的解大6,求
的解大6,求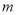 的值;
的值;(3)若关于
 的方程
的方程 与
与 均无解,求代数式
均无解,求代数式 的值.
的值. -
科目: 来源: 题型:
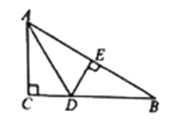
查看答案和解析>>【题目】如图,在△ABC,∠C=90°,AD平分∠BAC交CB于点D,过点D作DE⊥AB,垂足恰好是边AB的中点E.若AD=3cm,则BE的长为( )
A.
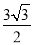 cmB. 4cmC. 3
cmB. 4cmC. 3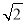 cmD. 6cm
cmD. 6cm
相关试题

