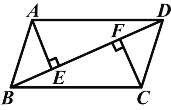
【题目】如图,已知在四边形ABCD中,AE⊥BD于E,CF⊥BD于F,AE=CF,BF=DE.求证:四边形ABCD是平行四边形.
参考答案:
【答案】见解析
【解析】
证明:证法一:∵BF=DE,
∴BF-EF=DE-EF,即BE=DF.
又∵AE⊥BD,CF⊥BD.
∴∠AEB=∠CFD=90°.
∵在△ABE和△CDF中,BE=DF,∠AEB=∠CFD,AE=CF,∴△ABE≌△CDF(SAS),∴AB=CD.
∵在△ADE和△CBF中,AE=CF,∠AED=∠BFC=90°,DE=BF,∴△ADE≌△CBF(SAS),∴AD=BC.
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形).
证法二:同证法一,得△ABE≌△CDF,
∴∠ABE=∠CDF,
∴AB∥CD.同理可证:AD∥BC,
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).
证法三:同证法一,得△ABE≌△CDF,
∴AB=CD,∠ABE=∠CDF,∴AB∥CD.
∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形).
证法四:连接AC,交BD于点O.
∵∠AEO=∠CFO=90°,∠AOE=∠COF,AE=CF.
∴△AOE≌△COF(AAS),∴AO=CO,EO=FO.
∵BF=DE,∴BE=DF,∴BE+EO=DF+FO,即BO=DO.
∴四边形ABCD是平行四边形(两条对角线互相平分的四边形是平行四边形).
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是
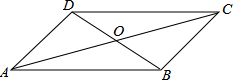
A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
-
科目: 来源: 题型:
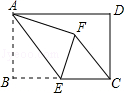
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )
A.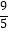
B.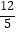
C.
D.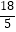
-
科目: 来源: 题型:
查看答案和解析>>【题目】珠海市某中学开展主题为“我爱阅读”的专题调查活动,为了解学校1200名学生一年内阅读书籍量,随机抽取部分学生进行统计,绘制成如下尚未完成的频数分布表和频数分布直方图.请根据图表,解答下面的问题:
分组
频数
频率
0≤x<5
4
0.08
5≤x<10
14
0.28
10≤x<15
16
a
15≤x<20
b
c
20≤x<25
10
0.2
合计
d
1.00
(1)a= ,b= c= .
(2)补全频数分布直方图;
(3)根据该样本,估计该校学生阅读书籍数量在15本或15本以上的人数.
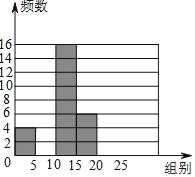
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=4,将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1 , 则阴影部分的面积为 .
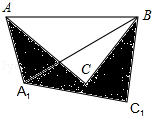
-
科目: 来源: 题型:
查看答案和解析>>【题目】潍坊到济南的距离约为210km,小刘开着小轿车,小张开着大货车,都从潍坊去济南,小刘比小张晚出发1小时,最后两车同时到达济南,已知小轿车的速度是大货车速度的1.5倍.
(1)求小轿车和大货车的速度各是多少?(列方程解答)
(2)当小刘出发时,求小张离济南还有多远? -
科目: 来源: 题型:
查看答案和解析>>【题目】今年是第39个植树节,我们提出了“追求绿色时尚,走向绿色文明”的倡议.某校为积极响应这一倡议,立即在八、九年级开展征文活动,校团委对这两个年级各班内的投稿情况进行统计,并制成了如图所示的两幅不完整的统计图.
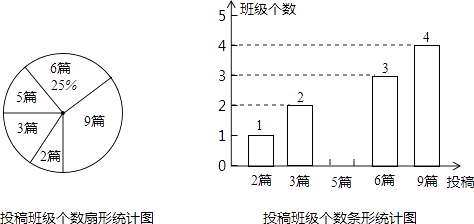
(1)求扇形统计图中投稿3篇的班级个数所对应的扇形的圆心角的度数.
(2)求该校八、九年级各班在这一周内投稿的平均篇数,并将该条形统计图补充完整.
(3)在投稿篇数最多的4个班中,八、九年级各有两个班,校团委准备从这四个班中选出两个班参加全校的表彰会,请你用列表法或画树状图的方法求出所选两个班正好不在同一年级的概率.
相关试题

