【题目】如图,△ABC中,∠C=90°,BC=7cm,AC=5,点P从B点出发,沿BC方向以2m/s的速度移动,点Q从C出发,沿CA方向以1m/s的速度移动.
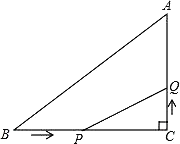
(1)若P、Q同时分别从B、C出发,那么几秒后,△PCQ的面积等于4?
(2)若P、Q同时分别从B、C出发,那么几秒后,PQ的长度等于5?
(3)△PCQ的面积何时最大,最大面积是多少?
参考答案:
【答案】(1)![]() 、
、![]() 秒;(2)
秒;(2)![]() 秒;(3)当t=
秒;(3)当t=![]() 时△PCQ的面积最大,最大面积为
时△PCQ的面积最大,最大面积为![]() .
.
【解析】
试题分析:(1)分别表示出线段CP和线段CQ的长,利用三角形的面积公式列出方程求解即可;
(2)表示出线段CP和CQ后利用勾股定理列出方程求解即可;
(3)列出△PCQ的面积关于t的函数解析式,配方可得最大值.
试题解析:(1)设t秒后△PCQ的面积等于4,根据题意得:CQ=t,BP=2t,则CP=7-2t,
![]() CQ×CP=
CQ×CP=![]() ×t(7-2t)=4,
×t(7-2t)=4,
整理,得:t1=![]() ,t2=
,t2=![]() ,
,
故若P、Q同时分别从B、C出发,那么![]() 、
、![]() 秒后,△PCQ的面积等于4;
秒后,△PCQ的面积等于4;
(2)若PQ的长度等于5,则PC2+QC2=PQ2,
即:(7-2t)2+t2=25,
整理,得:5t2-28t+24=0,
解得:t1=![]() ,t2=
,t2=![]() ,
,
∵CP=7-2t≥0,即t≤3.5,
∴t=![]() >3.5,舍去,
>3.5,舍去,
故那么![]() 秒后,PQ的长度等于5;
秒后,PQ的长度等于5;
(3)由(1)知△PCQ的面积S=![]() ×t(7-2t)=-(t-
×t(7-2t)=-(t-![]() )2+
)2+![]() ,
,
当t=![]() 时,S取得最大值,最大值为
时,S取得最大值,最大值为![]() ,
,
故当t=![]() 时△PCQ的面积最大,最大面积为
时△PCQ的面积最大,最大面积为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为1的小正方形网格中,△AOB的顶点均在格点上.

(1)B点关于y轴的对称点坐标为 ;
(2)将△AOB向左平移3个单位长度,再向上平移2个单位长度得到△A1O1B1,请画出△A1O1B1;
(3)在(2)的条件下,△AOB边AB上有一点P的坐标为(a,b),则平移后对应点P1的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校规划在一块长AD为18m,宽AB为13m的长方形场地ABCD上,设计分别与AD,AB平行的横向通道和纵向通道,其余部分铺上草皮.
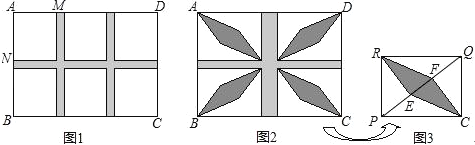
(1)如图1,若设计三条通道,一条横向,两条纵向,且它们的宽度相等,其余六块草坪相同,其中一块草坪两边之比AM:AN=8:9,问通道的宽是多少?
(2)为了建造花坛,要修改(1)中的方案,如图2,将三条通道改为两条通道,纵向的宽度改为横向宽度的2倍,其余四块草坪相同,且每一块草坪均有一边长为8m,这样能在这些草坪建造花坛.如图3,在草坪RPCQ中,已知RE⊥PQ于点E,CF⊥PQ于点F,求花坛RECF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.
(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求阴影部分的面积.(结果保留根号和π)

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中有稳定性的是( )
A. 长方形B. 多边形C. 锐角三角形D. 平行四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点P(a,2)与Q(﹣1,b)关于坐标原点对称,则a,b分别为( )
A.﹣1,2
B.1,﹣2
C.1,2
D.﹣1,﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中:(1)一个数,如果不是正数,必定就是负数;(2)整数与分数统称为有理数;(3)如果两个数的绝对值相等,那么这两个数相等;(4)符号不同的两个数互为相反数.其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

