【题目】如图![]() 是
是![]() 的中线,
的中线,![]() 是线段
是线段![]() 上一点(不与点
上一点(不与点![]() 重合),
重合),![]() 交
交![]() 于点
于点![]() ,
,![]() ,连结
,连结![]() .
.
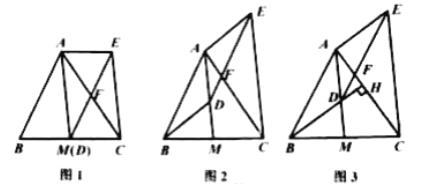
(1)如图1,当点![]() 与
与![]() 重合时,求证:四边形
重合时,求证:四边形![]() 是平行四边形;
是平行四边形;
(2)如图2,当点![]() 不与
不与![]() 重合时,(1)中的结论还成立吗?请说明理由.
重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,且
,且![]() .当
.当![]() ,
,![]() 时,求
时,求![]() 的长.
的长.
参考答案:
【答案】(1)详见解析;(2)结论成立,理由详见解析;(3)DH=1+![]() .
.
【解析】
试题分析:(1)由DE//AB,可得同位角相等:∠EDC=∠ABM,由CE//AM,可得同位角相等∠ECD=∠ADB,又由BD=DC,则△ABD△EDC,得到AB=ED,根据有一组对边平行且相等,可得四边形ABDE为平行四边形.(2)过点M作MG//DE交EC于点G,则可得四边形DMGE为平行四边形,且ED=GM且ED//GM,由(1)可得AB=GM且AB//GM,即可证得;(3)在已知条件中没有已知角的度数时,则在求角度时往特殊角30°,60°,45°的方向考虑,则要求这样的特殊角,就去找边的关系,构造直角三角形,取线段HC的中点I,连结MI,则MI是△BHC的中位线,可得MI//BH,MI=![]() BH,且MI⊥AC,则去找Rt△AMI中边的关系,求出∠CAM;设DH=x,即可用x分别表示出AH=
BH,且MI⊥AC,则去找Rt△AMI中边的关系,求出∠CAM;设DH=x,即可用x分别表示出AH=![]() x,AD=2x,AM=4+2x,BH=4+2x,由△HDF~△HBA,得到对应边成比例,求出x的值即可.
x,AD=2x,AM=4+2x,BH=4+2x,由△HDF~△HBA,得到对应边成比例,求出x的值即可.
试题解析:(1)证明:∵DE//AB,∴∠EDC=∠ABM,
∵CE//AM,
∴∠ECD=∠ADB,
又∵AM是△ABC的中线,且D与M重合,∴BD=DC,
∴△ABD△EDC,
∴AB=ED,又∵AB//ED,
∴四边形ABDE为平行四边形。
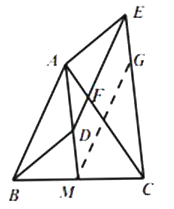
(2)解:结论成立,理由如下:
过点M作MG//DE交EC于点G,
∵CE//AM,
∴四边形DMGE为平行四边形,
∴ED=GM且ED//GM,
由(1)可得AB=GM且AB//GM,
∴AB=ED且AB//ED.
∴四边形ABDE为平行四边形.
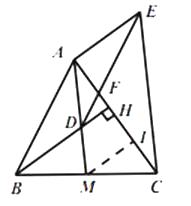
(3)
解:取线段HC的中点I,连结MI,
∴MI是△BHC的中位线,
∴MI//BH,MI=![]() BH,
BH,
又∵BH⊥AC,且BH=AM,
∴MI=![]() AM,MI⊥AC,
AM,MI⊥AC,
∴∠CAM=30°
设DH=x,则AH=![]() x,AD=2x,
x,AD=2x,
∴AM=4+2x,∴BH=4+2x,
由(2)已证四边形ABDE为平行四边形,
∴FD//AB,
∴△HDF~△HBA,
∴![]() , 即
, 即![]()
解得x=1±![]() (负根不合题意,舍去)
(负根不合题意,舍去)
∴DH=1+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某日的钱塘江观测信息如下:

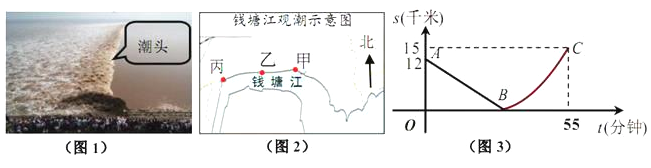
按上述信息,小红将“交叉潮”形成后潮头与乙地质检的距离
 (千米)与时间
(千米)与时间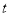 (分钟)的函数关系用图3表示.其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点
(分钟)的函数关系用图3表示.其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点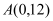 ,点
,点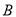 坐标为
坐标为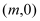 ,曲线
,曲线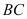 可用二次函数:s=
可用二次函数:s=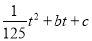 ,(
,(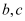 是常数)刻画.
是常数)刻画.(1)求
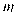 值,并求出潮头从甲地到乙地的速度;
值,并求出潮头从甲地到乙地的速度;(2)11:59时,小红骑单车从乙地出发,沿江边公路以
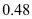 千米/分的速度往甲地方向去看潮,问她几分钟与潮头相遇?
千米/分的速度往甲地方向去看潮,问她几分钟与潮头相遇?(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为
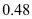 千米/分,小红逐渐落后.问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度
千米/分,小红逐渐落后.问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度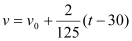 ,
, 是加速前的速度).
是加速前的速度). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
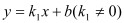 与反比例函数
与反比例函数 的图象交于点
的图象交于点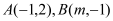 .
.(1)求这两个函数的表达式;
(2)在
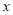 轴上是否存在点
轴上是否存在点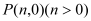 ,使
,使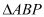 为等腰三角形?若存在,求
为等腰三角形?若存在,求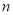 的值,若不存在,说明理由.
的值,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中点(-2,1)关于x轴的对称点的坐标为()
A. (-2,-1 ) B. (2,1) C. (-1,2) D. (1,-2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°.若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1∶0.75,坡长BC=10米,则此时AB的长约为(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)( )

A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算75°23′12″﹣46°53′43″=( )
A. 28°70′69″B. 28°30′29″C. 29°30′29″D. 28°29′29″
-
科目: 来源: 题型:
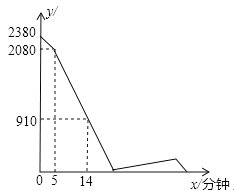
查看答案和解析>>【题目】A、B两地之间的路程为2380米,甲、乙两人分别从A、B两地出发,相向而行,已知甲先出发5分钟后,乙才出发,他们两人在A、B之间的C地相遇,相遇后,甲立即返回A地,乙继续向A地前行.甲到达A地时停止行走,乙到达A地时也停止行走,在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则乙到达A地时,甲与A地相距的路程是 米.
相关试题

