【题目】已知:二次函数y=﹣2x2+4x+m+1,与x轴的公共点为A,B.
(1)如果A与B重合,求m的值;
(2)横、纵坐标都是整数的点叫做整点:
①当m=﹣1时,求线段AB上整点的个数;
②若设抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)整点的个数为n,当1<n≤8时,结合函数的图象,求m的取值范围.
参考答案:
【答案】(1)-3(2)①当m=﹣1时,线段AB上整点的个数有3个②﹣3<m≤0
【解析】
(1)当A、B重合时,抛物线与x轴只有一个交点,此时△=0,从可求出m的值.
(2)①m=﹣1代入抛物线解析式,然后求出该抛物线与x轴的两个交点的坐标,从而可求出线段AB上的整点个数.
②由图象可得![]() ,即可求出m的取值范围.
,即可求出m的取值范围.
(1)∵A与B重合,
∴二次函数y=﹣2x2+4x+m+1的图象与x轴只有一个公共点,
∴方程﹣2x2+4x+m+1=0有两个相等的实数根,
∴△=42+4×2(m+1)=24+8m=0,
解得:m=﹣3.
∴如果A与B重合,m的值为-3.
(2)①当m=﹣1时,原二次函数为y=﹣2x2+4x+m+1=﹣2x2+4x,
令y=﹣2x2+4x=0,则x1=0,x2=2,
∴线段AB上的整点有(2,0)、(1,0)和(0,0).
故当m=﹣1时,线段AB上整点的个数有3个.
②二次函数![]() ,
,
当![]() 时,
时,![]()
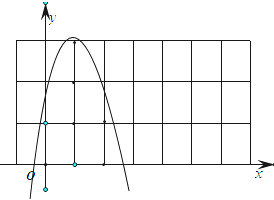
由点A,B之间的部分与线段AB所围成的区域内(包括边界)如图:
当![]() 时,
时,
∴![]()
∴![]() .
.
-
科目: 来源: 题型:
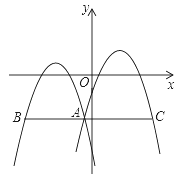
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=m(x+3)2+n与y=m(x﹣2)2+n+1交于点A.过点A作x轴的平行线,分别交两条抛物线于点B、C(点B在点C左侧),则线段BC的长为_____.
-
科目: 来源: 题型:
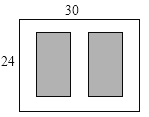
查看答案和解析>>【题目】如图,某小区有一块长为30 m,宽为24 m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480 m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为________m.
-
科目: 来源: 题型:
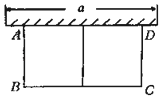
查看答案和解析>>【题目】如图,有长为30米的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可使用长度a=10米).设花圃的一边AB长为x米,面积为y平方米.
(1)求y与x的函数关系式并写出自变量x的取值范围;
(2)如果所围成的花圃的面积为63平方米,试求宽AB的长;
(3)按题目的设计要求, (填“能”或“不能”)围成面积为80平方米的花圃.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知关于x的方程2x2﹣mx﹣m2=0有一个根是1,求m的值;
(2)已知关于x的方程(2x﹣m)(mx+1)=(3x+1)(mx﹣1)有一个根是0,求另一个根和m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=2,AD=4,AC的垂直平分线EF交AD于点E、交BC于点F,则EF的长为( )
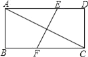
A. 4 B. 2
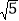 C.
C. 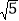 D. 2
D. 2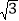
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了解学生对央视节目的观看情况,随机抽取了部分学生就“《国家宝藏》、《中国诗词大会》、《挑战不可能》、《欢乐中国人》这四个节目你看过几个“这个问题进行了问卷调查,被调查的每位同学可以在”0个、1个、2个、3个、4个“中选择一项,并根据调查结果进行数据整理后绘制出的不完整的统计图.

请根据图中的信息解答下列问题:
(1)补全条形统计图;
(2)所抽取学生观看节目个数的众数是 ;
(3)若该学校有2000人,请你估计该学校看过其中2个节目的学生人数是多少人?
相关试题

