【题目】如图,![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上一点且
边上一点且![]() ,点
,点![]() 是线段
是线段![]() 上一动点,连接
上一动点,连接![]() ,以
,以![]() 为斜边在
为斜边在![]() 的下方作等腰
的下方作等腰![]() ,当
,当![]() 从点
从点![]() 出发运动至点
出发运动至点![]() 停止时,点
停止时,点![]() 的运动路径长为__________.
的运动路径长为__________.
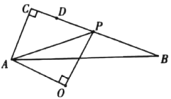
参考答案:
【答案】![]()
【解析】
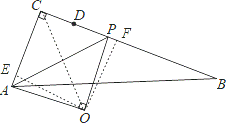
过O点作OE⊥CA于E,OF⊥BC于F,连接CO,如图,易得四边形OECF为矩形,由△AOP为等腰直角三角形得到OA=OP,∠AOP=90°,则可证明△OAE≌△OPF,所以AE=PF,OE=OF,根据角平分线的性质定理的逆定理得到CO平分∠ACP,从而可判断当P从点D出发运动至点B停止时,点O的运动路径为一条线段,接着证明CE=![]() (AC+CP),然后分别计算P点在D点和B点时OC的长,从而计算它们的差即可得到P从点D出发运动至点B停止时,点O的运动路径长.
(AC+CP),然后分别计算P点在D点和B点时OC的长,从而计算它们的差即可得到P从点D出发运动至点B停止时,点O的运动路径长.
过O点作OE⊥CA于E,OF⊥BC于F,连接CO,如图,
∵△AOP为等腰直角三角形,
∴OA=OP,∠AOP=90°,
∵∠CEO=∠CFO=∠ECF=90°,
∴四边形OECF为矩形,
∴∠EOF=90°,
∴∠AOE=∠POF,
又∵OA=OP,∠AEO=∠PFO=90°,
∴△OAE≌△OPF,
∴AE=PF,OE=OF,
∴四边形OECF是正方形,
∴CE=CF=OE,
∵OE=OF,OE⊥CA,OF⊥BC,
∴CO平分∠ACP,
∴当P从点D出发运动至点B停止时,点O的运动路径为一条线段,
∵AE=PF,
即AC﹣CE=CF﹣CP,
而CE=CF,
∴CE=![]() (AC+CP),
(AC+CP),
在Rt△OCE中,∠CEO=90°,∴CE2+OE2=OC2,
∴OC=![]() CE=
CE=![]() (AC+CP),
(AC+CP),
当AC=2,CP=CD=1时,OC=![]() ×(2+1)=
×(2+1)=![]() ,
,
当AC=2,CP=CB=5时,OC=![]() ×(2+5)=
×(2+5)=![]() ,
,
∴当P从点D出发运动至点B停止时,点O的运动路径长=![]() ﹣
﹣![]() =2
=2![]() ,
,
故答案为:2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】打折前,买6件A商品和3件B商品用了108元,买5件A商品和1件B商品用了84元,打折后买5件A商品和5件B商品用了80元。问打折后买5件A商品和5件B商品比不打折少花多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形
 中,
中,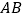 ∥
∥ ,
,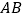 =2
=2 ,
, 为
为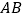 的中点,请仅用无刻度的直尺分别按下列要求画图(保留作图痕迹)
的中点,请仅用无刻度的直尺分别按下列要求画图(保留作图痕迹)(1)在图1中,画出△ABD的BD边上的中线;
(2)在图2中,若BA=BD, 画出△ABD的AD边上的高 .

-
科目: 来源: 题型:
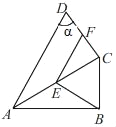
查看答案和解析>>【题目】如图,四边形ABCD中,AC平分∠BAD,∠ACD=∠ABC=90°,E、F分别为AC、CD的中点,∠D=α,则∠BEF的度数为_____(用含α的式子表示).
-
科目: 来源: 题型:
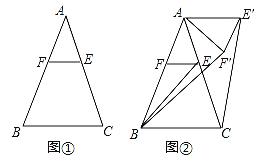
查看答案和解析>>【题目】已知,△ABC中,AB=AC,点E是边AC上一点,过点E作EF∥BC交AB于点F
(1)如图①,求证:AE=AF;
(2)如图②,将△AEF绕点A逆时针旋转α(0°<α<144°)得到△AE′F′.连接CE′BF′.
①若BF′=6,求CE′的长;
②若∠EBC=∠BAC=36°,在图②的旋转过程中,当CE′∥AB时,直接写出旋转角α的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为更好地践行社会主义核心价值观,让同学们珍惜粮食,学会感恩,校学生会积极倡导“光盘小行动”,某天午餐后学生会干部随机调查了部分同学就餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
(1)这次被调查的同学共有 名;
(2)补全条形统计图;
(3)计算在扇形统计图中剩大量饭菜所对应扇形圆心的度数;
(4)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供50人用一餐,据此估算,全校
 名学生一餐浪费的食物可供多少人食用一餐?
名学生一餐浪费的食物可供多少人食用一餐?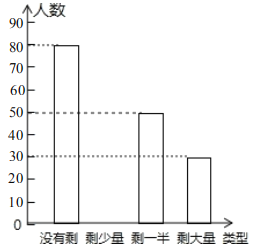

-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, 分别是
分别是 的中点,若等腰
的中点,若等腰 绕点
绕点 逆时针旋转,得到等腰
逆时针旋转,得到等腰 ,设旋转角为
,设旋转角为 ,记直线
,记直线 与
与 的交点为
的交点为


(1)如图
 ,当
,当 时,线段
时,线段 的长等于 ,线段
的长等于 ,线段 的长等于 .(直接填写结果)
的长等于 .(直接填写结果)(2)如图
 ,当
,当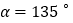 时,求证:
时,求证: ,且
,且 ;
;(3)设
 的中点为
的中点为 ,则线段
,则线段 的长为 (直接填写结果).
的长为 (直接填写结果).
相关试题

