【题目】如图,在正方形ABCD中,点E在边CD上
(1)以A为中心,把△ADE按顺时针方向旋转90°,画出旋转后的图形;
(2)设旋转后点E的对应点为F,连接EF,△AEF是什么三角形
(3)若四边形AECF的面积为25,DE=2,求AE的长

参考答案:
【答案】(1)见解析;(2)△AEF是等腰直角三角形;(3)![]()
【解析】
(1)利用正方形的性质,可画出旋转后的图形;
(2)由旋转的性质,可得AF=AE,∠FAE=90°,即△AEF是等腰直角三角形的性质.
(3)由四边形AECF的面积为25,易知正方形的面积也为25,从而得到正方形的边长AD=5,而DE=2,再利用勾股定理即可求出AE.
解:(1)如图,△ABF即是旋转后的图形;

(2)△AEF是等腰直角三角形.
理由:∵以A为中心,把△ADE按顺时针方向旋转90°得到△ABF,
∴AF=AE,∠FAE=90°,
∴△AEF是等腰直角三角形的性质.
(3)∵△ADE≌△ABF,
∴![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在Rt![]() 中,DE=2,AD=5,
中,DE=2,AD=5,
∴![]() ,
,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知
 ABC的三个顶点的坐标分别为A(-1,1),B(-3,1),C(-1,4).
ABC的三个顶点的坐标分别为A(-1,1),B(-3,1),C(-1,4).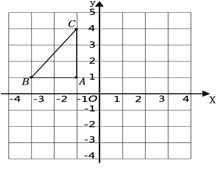
(1)画出△ABC关于y轴对称的图形;
(2)将△ABC绕着点B顺时针旋转90°后得到△A2BC2,请在图中画出△A2BC2,并求出线段BC旋转过程中所扫过的面积(结果保留
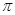 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学举行电脑知识竞赛,将八年级两个班参赛学生的成绩(得分均为整数)进行整理后,分成5组,绘制出如下的频数分布直方图(如图),已知图中从左到右的第一、第三、第四、第五小组的频率分别为0.30、0.15、0.10、0.05,第二组的频数是40
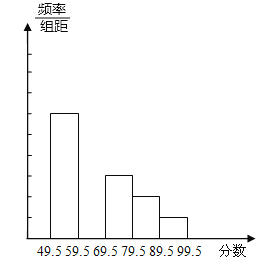
(1)求第二组的频率,并补全这个频数分布直方图;
(2)这两个班参赛的学生人数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P从
 出发,沿所示方向运动,每当碰到长方形OABC的边时会进行反弹,反弹时反射角等于入射角,当点P第2018次碰到长方形的边时,点P的坐标为______.
出发,沿所示方向运动,每当碰到长方形OABC的边时会进行反弹,反弹时反射角等于入射角,当点P第2018次碰到长方形的边时,点P的坐标为______.
【答案】

【解析】
根据反射角与入射角的定义作出图形;由图可知,每6次反弹为一个循环组依次循环,用2018除以6,根据商和余数的情况确定所对应的点的坐标即可.
解:如图所示:经过6次反弹后动点回到出发点
 ,
,
 ,
, 当点P第2018次碰到矩形的边时为第337个循环组的第2次反弹,
当点P第2018次碰到矩形的边时为第337个循环组的第2次反弹, 点P的坐标为
点P的坐标为 .
.故答案为:
 .
.【点睛】
此题主要考查了点的坐标的规律,作出图形,观察出每6次反弹为一个循环组依次循环是解题的关键.
【题型】填空题
【结束】
15【题目】为了保护环境,某公交公司决定购买A、B两种型号的全新混合动力公交车共10辆,其中A种型号每辆价格为a万元,每年节省油量为
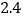 万升;B种型号每辆价格为b万元,每年节省油量为
万升;B种型号每辆价格为b万元,每年节省油量为 万升:经调查,购买一辆A型车比购买一辆B型车多20万元,购买2辆A型车比购买3辆B型车少60万元.
万升:经调查,购买一辆A型车比购买一辆B型车多20万元,购买2辆A型车比购买3辆B型车少60万元. 请求出a和b;
请求出a和b; 若购买这批混合动力公交车每年能节省
若购买这批混合动力公交车每年能节省 万升汽油,求购买这批混合动力公交车需要多少万元?
万升汽油,求购买这批混合动力公交车需要多少万元? -
科目: 来源: 题型:
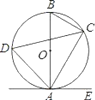
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
(1)求∠ABC的度数;
(2)求证:AE是⊙O的切线;
(3)当BC=4时,求劣弧AC的长.
-
科目: 来源: 题型:
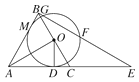
查看答案和解析>>【题目】如图,△ABC是等边三角形,AO⊥BC,垂足为点O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G,F两点.
(1)求证:AB与⊙O相切;
(2)若AB=4,求线段GF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0)、(2,0)、(2,1)、(3,1)、(3,0)、(3,﹣1)、…,根据这个规律探索可得,第220个点的坐标为_____.

相关试题

