【题目】如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;② ![]() ;③△PMN为等边三角形;④当∠ABC=45°时,BN=
;③△PMN为等边三角形;④当∠ABC=45°时,BN= ![]() PC.其中正确的个数是( )
PC.其中正确的个数是( ) 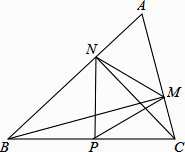
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】D
【解析】解:①∵BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点, ∴PM= ![]() BC,PN=
BC,PN= ![]() BC,
BC,
∴PM=PN,正确;
②在△ABM与△ACN中,
∵∠A=∠A,∠AMB=∠ANC=90°,
∴△ABM∽△ACN,
∴ ![]() ,正确;
,正确;
③∵∠A=60°,BM⊥AC于点M,CN⊥AB于点N,
∴∠ABM=∠ACN=30°,
在△ABC中,∠BCN+∠CBM═180°﹣60°﹣30°×2=60°,
∵点P是BC的中点,BM⊥AC,CN⊥AB,
∴PM=PN=PB=PC,
∴∠BPN=2∠BCN,∠CPM=2∠CBM,
∴∠BPN+∠CPM=2(∠BCN+∠CBM)=2×60°=120°,
∴∠MPN=60°,
∴△PMN是等边三角形,正确;
④当∠ABC=45°时,∵CN⊥AB于点N,
∴∠BNC=90°,∠BCN=45°,
∴BN=CN,
∵P为BC边的中点,
∴PN⊥BC,△BPN为等腰直角三角形
∴BN= ![]() PB=
PB= ![]() PC,正确.
PC,正确.
故选D.
【考点精析】通过灵活运用等边三角形的判定和直角三角形斜边上的中线,掌握三个角都相等的三角形是等边三角形;有一个角等于60°的等腰三角形是等边三角形;直角三角形斜边上的中线等于斜边的一半即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于下列结论: ①二次函数y=6x2 , 当x>0时,y随x的增大而增大.
②关于x的方程a(x+m)2+b=0的解是x1=﹣2,x2=1(a、m、b均为常数,a≠0),则方程a(x+m+2)2+b=0的解是x1=﹣4,x2=﹣1.
③设二次函数y=x2+bx+c,当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0,那么c的取值范围是c≥3.
其中,正确结论的个数是( )
A.0个
B.1个
C.2个
D.3个 -
科目: 来源: 题型:
查看答案和解析>>【题目】一辆货车从百货大楼出发负责送货,向东走了 5 千米到达小明家,继续向东走了 1.5 千米到达小红家,然后向西走了 9.5 千米到达小刚家,最后返回百货大楼.

(1)以百货大楼为原点,向东为正方向,1 个单位长度表示 1 千米,请你在数轴上标出小明、小红、小刚家的位置.(小明家用点 A 表示,小红家用点 B 表示,小刚家用点 C 表示)
(2)小明家与小刚家相距多远?
(3)若货车每千米耗油 0.6 升,那么这辆货车此次送货共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某市举办的“读好书,讲礼仪”活动中,东华学校积极行动,各班图书角的新书、好书不断增多,除学校购买外,还有师生捐献的图书.下面是七年级(1)班全体同学捐献图书的情况统计图:
请你根据以上统计图中的信息,解答下列问题:
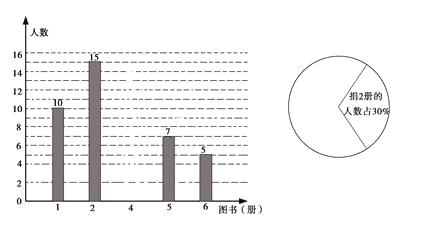
(1)该班有学生多少人?
(2)补全条形统计图;
(3)七(1)班全体同学所捐献图书的中位数和众数分别是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,AD=12,过点A、D两点的⊙O与BC边相切于点E,则⊙O的半径为 .
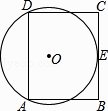
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东30°方向以每小时10海里的速度航行,甲沿南偏西75°方向以每小时10
 海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.则甲船追赶乙船的速度为海里/小时?
海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.则甲船追赶乙船的速度为海里/小时?
-
科目: 来源: 题型:
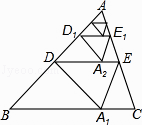
查看答案和解析>>【题目】如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1 , 还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2017次操作后得到的折痕D2016E2016 , 到BC的距离记为h2017;若h1=1,则h2017的值为 .
相关试题

