【题目】如图,四边形ABCD中,DC∥AB ,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=2时,求AE的长.

参考答案:
【答案】(1)证明见解析;(2)6.
【解析】试题分析:(1)根据已知条件易证△OBE≌△ODF,根据全等三角形的性质即可得结论;(2)根据已知条件易证∠G=∠A=45°,由等腰三角形的性质可得AE=GE,再证得DG=DO,即可得OF=FG= 2,再由(1)可知OE= OF=2,所以GE=OE+OF+FG=6,即AE= GE=6.
试题解析:
(1)证明:∵ DC∥AB, ∴∠OBE =∠ODF.
在△OBE与△ODF中,
∵ 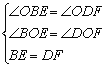
∴△OBE≌△ODF(AAS).
∴BO=DO.
(2)∵EF⊥AB,DC∥AB,
∴∠GEA=∠GFD=90°.
∵∠A=45°,∴∠G=∠A=45°.
∴AE=GE,
∵BD⊥AD, ∴∠ADB=∠GDO=90°.
∴∠GOD=∠G=45°.
∴DG=DO,
∴OF=FG= 2,
由(1)可知,OE= OF=2,
∴GE=OE+OF+FG=6
∴AE= GE=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年1月至8月,某市汽车产量为80万辆,其中80万用科学记数法表示为( )
A.8×104B.0.8×105C.8×106D.8×105
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,BC=2,AB=AC=4,点D是BC的中点,E为AC的中点,点P为AB上的动点,则点D到AC的距离为_____,DP+EP的最小值等于_____.
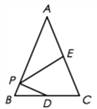
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的三线段,能组成等腰三角形的是 ( )
A. 1cm 1cm 2cm B. 2cm 2 cm 5 cm
C. 3cm 3cm 5cm D. 3cm 4cm 5cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=﹣2x2﹣1向上平移若干个单位,使抛物线与坐标轴有三个交点,如果这些交点能构成直角三角形,那么平移的距离为( )
A.
 个单位 B.1个单位
个单位 B.1个单位 C.
 个单位 D.
个单位 D.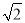 个单位
个单位 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. a3a2=a5 B. (a2)3=a5 C. a3+a3=a6 D. (a+b)2=a2+b2
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的两边长分别是4cm和6cm,则它的周长是_________.
相关试题

