【题目】如图①点A,B,C,D在同一直线上,AB=CD,作CE⊥AD,BF⊥AD,且AE=DF. 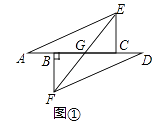
(1)证明:EF平分线段BC;
(2)若△BFD沿AD方向平移得到图②时,其他条件不变,(1)中的结论是否仍成立?请说明理由. 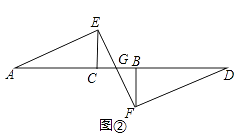
参考答案:
【答案】
(1)证明:∵CE⊥AD,BF⊥AD,
∴∠ACE=∠DBF=90°,
∵AB=CD,
∴AB+BC=BC+CD,即AC=DB,
在Rt△ACE和Rt△DBF中,
![]() ,
,
∴Rt△ACE≌Rt△DBF(HL),
∴CE=FB,
在△CEG和△BFG中,
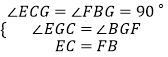 ,
,
∴△CEG≌△BFG(AAS),
∴CG=BG,即EF平分线段BC;
(2)(1)中结论成立,理由为:
证明:∵CE⊥AD,BF⊥AD,
∴∠ACE=∠DBF=90°,
∵AB=CD,
∴AB﹣BC=CD﹣BC,即AC=DB,
在Rt△ACE和Rt△DBF中,
![]() ,
,
∴Rt△ACE≌Rt△DBF(HL),
∴CE=FB,
在△CEG和△BFG中,
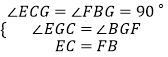 ,
,
∴△CEG≌△BFG(AAS),
∴CG=BG,即EF平分线段BC.
【解析】(1)由AB=CD,利用等式的性质得到AC=BD,再由AE=DF,利用HL得到直角三角形ACE与直角三角形DBF全等,利用全等三角形对应边相等得到EC=BF,再利用AAS得到三角形ECG与三角形FBG全等,利用全等三角形对应边相等得到BG=CG,即可得证;(2)(1)中的结论成立,理由为:由AC=DB,利用等式的性质得到AC=BD,再由AE=DF,利用HL得到直角三角形ACE与直角三角形DBF全等,利用全等三角形对应边相等得到EC=BF,再利用AAS得到三角形ECG与三角形FBG全等,利用全等三角形对应边相等得到BG=CG,即可得证.
【考点精析】通过灵活运用平移的性质,掌握①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某建筑工程队利用一面墙(墙的长度不限),用40米长的篱笆围成一个长方形的仓库.
(1)求长方形的面积是150平方米,求出长方形两邻边的长;
(2)能否围成面积220平方米的长方形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC,∠A=36°,AB的中垂线交AC于点E,交AB于点D,下面4个结论:
①射线BE是∠ABC的平分线;②△BCE是等腰三角形;③△ABE是等腰三角形;④△ADE≌△BDE;
(1)判断其中正确的结论是哪几个?
(2)从你认为是正确的结论中选一个加以说明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的角平分线,则图中的等腰三角形有( )

A. 5个 B. 4个 C. 3个 D. 2个
-
科目: 来源: 题型:
查看答案和解析>>【题目】若﹣x3ym与2yx3是同类项,则m的值是( )
A. ﹣1 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣2,3,0,﹣1中,最小的数是( )
A. ﹣2B. 3C. 0D. ﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年浙江省生产总值约为56200亿元.数56200用科学记数法表示为( )
A. 56.2×103B. 5.62×104C. 562×102D. 0.562×103
相关试题

