【题目】如图,已知直线l1∥l2 , 直线l和直线l1、l2分别交于点C和D,在直线l上有一点P(点P与点C,D不重合),点A在直线l1上,点B在直线l2上. 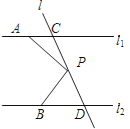
(1)当点P在C,D之间运动时,试说明:∠PAC+∠PBD=∠APB;
(2)当点P在直线l1的上方运动时,试探索∠PAC、∠APB、∠PBD之间的关系又是如何?为什么?
参考答案:
【答案】
(1)解:如图,延长AP交DB于H,
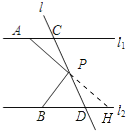
∵AC∥BH,
∴∠PAC=∠PHB,
∵∠APB=∠PBD+∠PHB,
∴∠APB=∠PAC+∠PBD
(2)解:如图,∠PBD=∠PAC+∠APB.
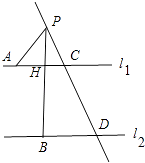
理由:∵AC∥BD,
∴∠PHC=∠PBD,
∵∠PHC=∠PAC+∠APB,
∴∠PBD=∠APB+∠PAC
【解析】(1)延长AP交DB于H,根据平行线的性质以及三角形外角的性质即可解决问题.(2)结论:,∠PBD=∠PAC+∠APB.证明方法类似
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠α的补角为125°12′,则它的余角为( )
A.35°12′
B.35°48′
C.55°12′
D.55°48′ -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题的个数( )
(1)⊙O的半径为5,点P在直线l上,且OP=5,则直线l与⊙O相切
(2)在Rt△ABC中,∠C=90°,AC=5,BC=12,则△ABC的外接圆半径为6.5
(3)正多边形都是轴对称图形,也都是中心对称图形
(4)三角形的外心到三角形各边的距离相等.
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】用公式法解方程6x-8=5x2时,a、b、c的值分别是( )
A.5、6、-8
B.5、-6、-8
C.5、-6、8 D . 6、5、-8 -
科目: 来源: 题型:
查看答案和解析>>【题目】用公式法解方程5x2=6x-8时,a、b、c的值分别是( )
A.5、6、-8
B.5、-6、-8
C.5、-6、8
D.6、5、-8 -
科目: 来源: 题型:
查看答案和解析>>【题目】某电动自行车厂三月份的产量为1000辆,由于市场需求量不断增大,五月份的产量提高到1210辆,该厂四、五、六月份的月平均增长率相同,那么六月份的产量为__________辆.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)
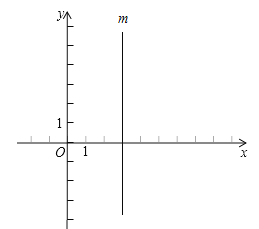
如图,在直角坐标平面内,已知点A(8,0),点B(3,0),点C是点A关于直线m(直线m上各点的横坐标都为3)的对称点.
(1)在图中标出点A,B,C的位置,并求出点C的坐标;
(2)如果点P在y轴上,过点P作直线l∥x轴,点A关于直线l的对称点是点D,那么当△BCD的面积等于15时,求点P的坐标.
相关试题

